Author: Dr. Judson Ryckman, Clemson University
This notebook builds a pSi square-grating guided-mode-resonance (GMR) reflector in Tidy3D, visualizes the geometry, runs a cloud simulation, and plots the reflection spectrum.
Notes:
- This model allows for simulation of an anisotropic material in the core and cladding using either a non-dispersive, user specified material, or a pre-fitted dispersive material model.
[1]:
import matplotlib.pyplot as plt
import numpy as np
import tidy3d as td
import tidy3d.web as web
[2]:
# Define geometry (microns)
period = 0.5
wl_min = 0.4
wl_max = 0.8
size_z = 3
gap = 0.15
slab_thick = 0.09
etch_depth = 0.15
cd_bias = 0.045
duty_cycle = 0.5 + cd_bias / period
[3]:
use_dispersive_material_model = True # True or False
# If using non-dispersive model
n_core = 1.54
n_clad = 1.19
delta_n = 0.05
k_core = 0.005
# Define background medium
Vacuum = td.Medium(
name="Vacuum",
)
[4]:
# Define anisotropic materials (dispersive or non-dispersive)
if use_dispersive_material_model:
# --- Dispersive material model ---
anisotropic_cladding = td.AnisotropicMedium(
name="anisotropic_cladding",
xx=td.PoleResidue(
name="clad_ORD_p78_sp65_sigma45",
frequency_range=[374740572500000, 749481145000000],
eps_inf=1.285763200610988,
poles=[
[
(-80006430873749.78 - 3992826532935084.5j),
(43225975831.18877 + 65698194005.3712j),
],
[
(-254779968980075.38 - 6210018855903866j),
(26447240584513.562 + 322970863925251.1j),
],
],
),
yy=td.PoleResidue(
name="clad_ORD_p78_sp65_sigma45",
frequency_range=[374740572500000, 749481145000000],
eps_inf=1.285763200610988,
poles=[
[
(-80006430873749.78 - 3992826532935084.5j),
(43225975831.18877 + 65698194005.3712j),
],
[
(-254779968980075.38 - 6210018855903866j),
(26447240584513.562 + 322970863925251.1j),
],
],
),
zz=td.PoleResidue(
name="clad_EXT_p78_sp65_sigma45",
frequency_range=[374740572500000, 749481145000000],
eps_inf=1.3638432159648597,
poles=[
[
(-225020803639667.75 - 5894420287418583j),
(40348009572759.95 + 529332098674452.8j),
],
[
(-70804109316383.19 - 4024765445948748.5j),
(49573077608.54553 + 214392902555.40454j),
],
[
(-31856302596180.74 - 4185043474496780.5j),
(17457996399.55387 - 11843520333.727072j),
],
],
),
)
anisotropic_core = td.AnisotropicMedium(
name="anisotropic_core",
xx=td.PoleResidue(
name="core_ORD_p60_sp50_sigma18",
frequency_range=[374740572500000, 749481145000000],
eps_inf=1.7636879320933365,
poles=[
[
(-209812302659551.34 - 5713050507260843j),
(91645423757352.25 + 1245780204707888.5j),
],
[
(-33767895447480.945 - 4076300334074186.5j),
(-383042439354.49066 + 74306357834.59213j),
],
[
(-118113417687026.97 - 4102291974502630.5j),
(433192944675.4037 + 920226300587.0059j),
],
],
),
yy=td.PoleResidue(
name="core_ORD_p60_sp50_sigma18",
frequency_range=[374740572500000, 749481145000000],
eps_inf=1.7636879320933365,
poles=[
[
(-209812302659551.34 - 5713050507260843j),
(91645423757352.25 + 1245780204707888.5j),
],
[
(-33767895447480.945 - 4076300334074186.5j),
(-383042439354.49066 + 74306357834.59213j),
],
[
(-118113417687026.97 - 4102291974502630.5j),
(433192944675.4037 + 920226300587.0059j),
],
],
),
zz=td.PoleResidue(
name="core_EXT_p60_sp50_sigma18",
frequency_range=[374740572500000, 749481145000000],
eps_inf=1.8442541496138387,
poles=[
[
(-194036164426216.44 - 5575364239486789j),
(104804935602979.1 + 1468449074428882j),
],
[
(-139501019944869.6 - 4570504481783418j),
(-1034474504270.1329 - 626357243110.9268j),
],
[
(-47718826616363.5 - 4342881289958674.5j),
(-370871032855.6184 + 122560276380.73393j),
],
[
(-19150839534338.004 - 3934925705165841j),
(-2319448769.6423297 - 85365662359.27574j),
],
[
(-53127023418600.734 - 4039267182350066j),
(-169960900226.993 + 815175929541.1998j),
],
],
),
)
else:
# --- Non-dispersive material model ---
anisotropic_cladding = td.FullyAnisotropicMedium(
name="anisotropic_cladding",
permittivity=[
[n_clad**2 - k_core**2, 0, 0],
[0, n_clad**2 - k_core**2, 0],
[0, 0, (n_clad + delta_n) ** 2 - k_core**2],
],
conductivity=[
[0.0526 * n_clad * k_core, 0, 0],
[0, 0.0526 * n_clad * k_core, 0],
[0, 0, 0.0526 * (n_clad + delta_n) * k_core],
],
)
anisotropic_core = td.FullyAnisotropicMedium(
name="anisotropic_core",
permittivity=[
[n_core**2 - k_core**2, 0, 0],
[0, n_core**2 - k_core**2, 0],
[0, 0, (n_core + delta_n) ** 2 - k_core**2],
],
conductivity=[
[0.0526 * n_core * k_core, 0, 0],
[0, 0.0526 * n_core * k_core, 0],
[0, 0, 0.0526 * (n_core + delta_n) * k_core],
],
)
[5]:
# Define frequency and wavelength range
lda0 = 0.6
freq0 = td.C_0 / lda0
ldas = np.linspace(0.4, 0.8, 701)
freqs = td.C_0 / ldas
fwidth = 0.5 * (np.max(freqs) - np.min(freqs))
# Add source
plane_wave = td.PlaneWave(
name="plane_wave",
center=[0, 0, size_z / 2 - wl_max / 2],
size=[td.inf, td.inf, 0],
source_time=td.GaussianPulse(
freq0=freq0,
fwidth=fwidth,
),
direction="-",
)
# Add monitors
Reflection = td.FluxMonitor(
name="Reflection",
center=[0, 0, size_z / 2 - wl_max / 4],
size=[100, 100, 0],
freqs=freqs,
)
field_XZ = td.FieldMonitor(name="field_XZ", size=[period, 0, size_z], freqs=freqs[::5])
field_YZ = td.FieldMonitor(name="field_YZ", size=[0, period, size_z], freqs=freqs[::5])
[6]:
# Define structures
substrate = td.Structure(
name="substrate",
geometry=td.Box(center=[0, 0, -500], size=[2000, 2000, 1000]),
medium=anisotropic_cladding,
)
core_slab = td.Structure(
name="core_slab",
geometry=td.Box(center=[0, 0, slab_thick / 2], size=[5, 5, slab_thick]),
medium=anisotropic_core,
)
temp_pillar = td.Structure(
name="temp_pillar",
geometry=td.Box(
center=[0, 0, slab_thick / 2],
size=[period * duty_cycle, period * duty_cycle, slab_thick],
),
medium=anisotropic_cladding,
)
cylinder_N = td.Structure(
geometry=td.Cylinder(
axis=0,
radius=slab_thick,
center=[0, period * duty_cycle / 2, slab_thick],
length=duty_cycle * period,
),
name="cylinder_N",
medium=anisotropic_core,
)
cylinder_S = td.Structure(
geometry=td.Cylinder(
axis=0,
radius=slab_thick,
center=[0, -period * duty_cycle / 2, slab_thick],
length=duty_cycle * period,
),
name="cylinder_S",
medium=anisotropic_core,
)
cylinder_E = td.Structure(
geometry=td.Cylinder(
axis=1,
radius=slab_thick,
center=[period * duty_cycle / 2, 0, slab_thick],
length=duty_cycle * period,
),
name="cylinder_E",
medium=anisotropic_core,
)
cylinder_W = td.Structure(
geometry=td.Cylinder(
axis=1,
radius=slab_thick,
center=[-period * duty_cycle / 2, 0, slab_thick],
length=duty_cycle * period,
),
name="cylinder_W",
medium=anisotropic_core,
)
temp_pillar_slab = td.Structure(
name="temp_pillar_slab",
geometry=td.Box(
center=[0, 0, slab_thick + etch_depth / 2], size=[5, 5, etch_depth]
),
medium=Vacuum,
)
core_pillar = td.Structure(
name="core_pillar",
geometry=td.Box(
center=[0, 0, slab_thick + etch_depth / 2],
size=[period * duty_cycle, period * duty_cycle, etch_depth],
),
medium=anisotropic_core,
)
internal_pillar = td.Structure(
name="internal_pillar",
geometry=td.Box(
center=[0, 0, slab_thick + etch_depth / 2 - slab_thick],
size=[
(period * duty_cycle - 2 * slab_thick)
* ((period * duty_cycle - 2 * slab_thick) > 0),
(period * duty_cycle - 2 * slab_thick)
* ((period * duty_cycle - 2 * slab_thick) > 0),
etch_depth,
],
),
medium=anisotropic_cladding,
)
pillar_cap = td.Structure(
name="pillar_cap",
geometry=td.Box(
center=[0, 0, slab_thick + etch_depth + 0.3], size=[period * 4, period * 4, 0.6]
),
medium=Vacuum,
)
[7]:
# Build simulation
sim = td.Simulation(
size=[0.5, 0.5, 3],
boundary_spec=td.BoundarySpec(
x=td.Boundary.periodic(), y=td.Boundary.periodic(), z=td.Boundary.pml()
),
grid_spec=td.GridSpec.auto(min_steps_per_wvl=24, wavelength=np.min(ldas)),
shutoff=1e-8,
run_time=5e-12,
medium=Vacuum,
sources=[plane_wave],
monitors=[Reflection, field_XZ, field_YZ],
structures=[
substrate,
core_slab,
temp_pillar,
cylinder_N,
cylinder_S,
cylinder_E,
cylinder_W,
temp_pillar_slab,
core_pillar,
internal_pillar,
pillar_cap,
],
)
[8]:
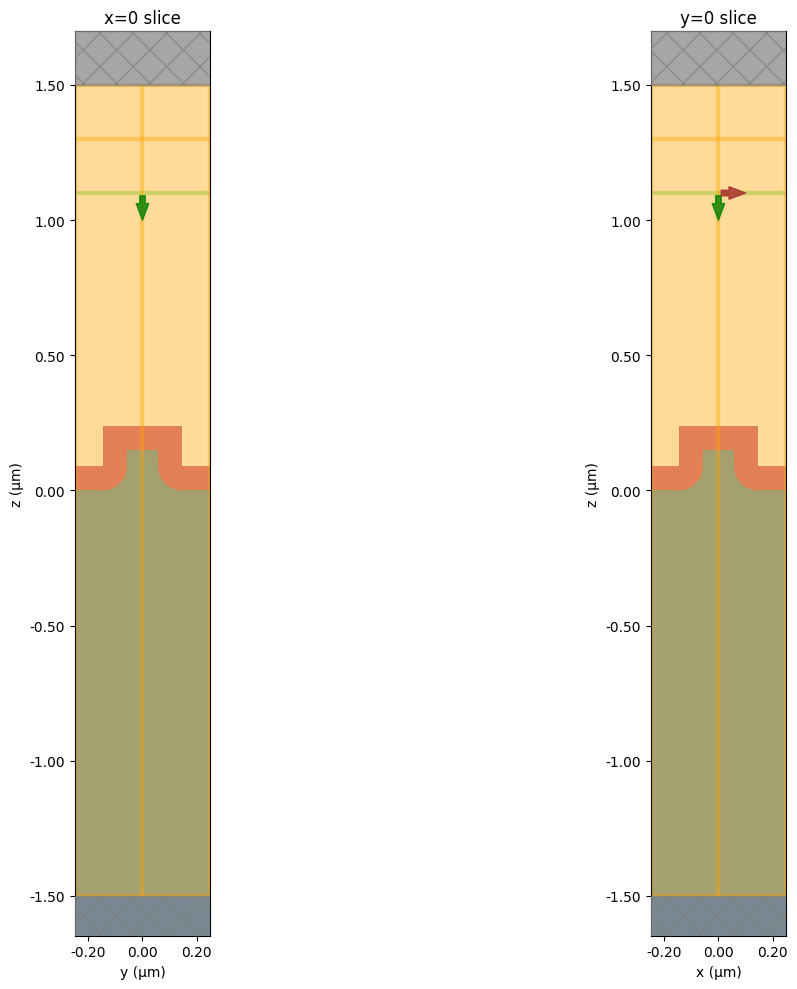
# Visualize 2D cross sections of device geometry
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 10))
sim.plot(x=0.0, ax=ax1)
ax1.set_title("x=0 slice")
# sim.plot_grid(x=0, ax=ax1) # Optional to inspect grid
sim.plot(y=0.0, ax=ax2)
ax2.set_title("y=0 slice")
# sim.plot_grid(y=0, ax=ax2) # Optional to inspect grid
plt.tight_layout()
plt.show()
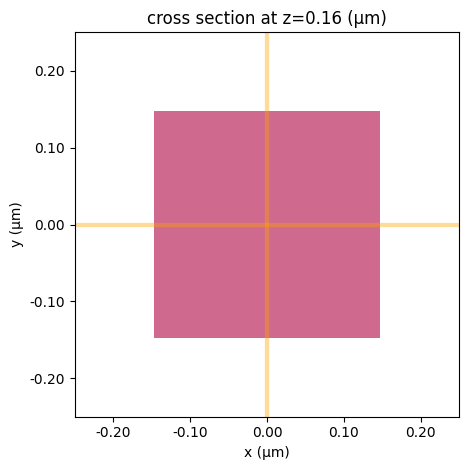
ax3 = sim.plot(z=slab_thick + etch_depth / 2)
# sim.plot_grid(x=0, ax=ax)
plt.show()
[9]:
# Visualize simulation in 3D
sim.plot_3d()
[10]:
# Run the simulation
sim_data = web.run(
sim,
task_name="curved_pSi_GMR_Dispersive_Anisotropic_FIG2_FDTD",
path="./data/sim_data.hdf5",
)
10:43:09 Eastern Daylight Time Created task 'curved_pSi_GMR_Dispersive_Anisotropic_FIG2_FDTD' with task_id 'fdve-73d81855-284a-498e-9cbc-73546516497d' and task_type 'FDTD'.
View task using web UI at 'https://tidy3d.simulation.cloud/workbench?taskId =fdve-73d81855-284a-498e-9cbc-73546516497d'.
Task folder: 'default'.
Output()
10:43:11 Eastern Daylight Time Maximum FlexCredit cost: 0.333. Minimum cost depends on task execution details. Use 'web.real_cost(task_id)' to get the billed FlexCredit cost after a simulation run.
status = queued
To cancel the simulation, use 'web.abort(task_id)' or 'web.delete(task_id)' or abort/delete the task in the web UI. Terminating the Python script will not stop the job running on the cloud.
Output()
10:43:18 Eastern Daylight Time starting up solver
running solver
Output()
10:44:29 Eastern Daylight Time early shutoff detected at 44%, exiting.
status = postprocess
Output()
10:44:35 Eastern Daylight Time status = success
10:44:37 Eastern Daylight Time View simulation result at 'https://tidy3d.simulation.cloud/workbench?taskId =fdve-73d81855-284a-498e-9cbc-73546516497d'.
Output()
10:44:43 Eastern Daylight Time loading simulation from ./data/sim_data.hdf5
[11]:
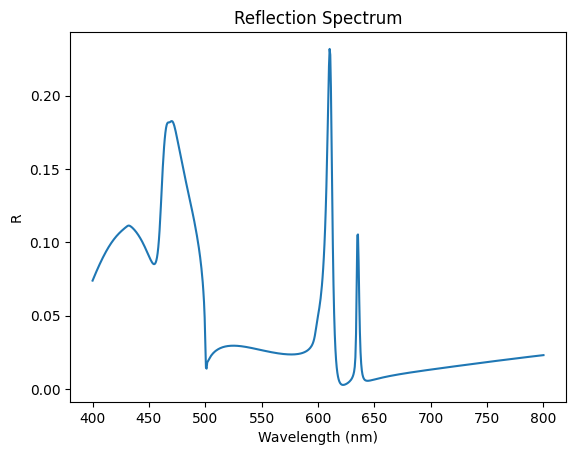
# Select reflection monitor by its name in your sim
plot_data = sim_data[
"Reflection"
].flux # Adjust "Reflection" if your monitor has a different name
flux_vals = np.abs(plot_data.values)
plt.figure()
plt.plot(ldas * 1e3, flux_vals)
plt.xlabel("Wavelength (nm)")
plt.ylabel("R")
plt.title("Reflection Spectrum")
# plt.gca().invert_xaxis() # optional: decreasing wavelength left-to-right
plt.show()
[12]:
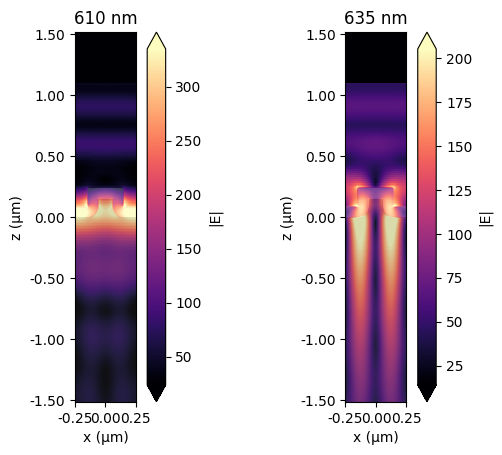
# Plot field distributions at the resonances at around 610 nm and 635 nm for example
fig, ax = plt.subplots(1, 2)
idx = np.abs(ldas - 0.61).argmin()
sim_data.plot_field("field_XZ", "E", "abs", f=freqs[idx], ax=ax[0])
ax[0].set_title("610 nm")
idx = np.abs(ldas - 0.635).argmin()
sim_data.plot_field("field_XZ", "E", "abs", f=freqs[idx], ax=ax[1])
ax[1].set_title("635 nm")
plt.show()
[ ]:
TERMS & CONDITIONS
How the process works:
Try this real URL to see an example: