In this tutorial, we demonstrate how to translate the absorption coefficient parameter ($\alpha$ [$\text{cm}^{-1}$]) into a Tidy3D Medium and calculate volumetric power absorption using a 3D FieldMonitor and PermittivityMonitor.

Creating a Lossy Medium¶

Tidy3D follows the $e^{-\omega t}$ convention, in which losses are represented by a positive imaginary part of the refractive index, here denoted as $k$:

$\tilde{n} = n + i k$

We can relate $k$ to the absorption coefficient from the Beer-Lambert law:

$I = I_0 e^{-\alpha z}$

where:

$k = \frac{\lambda \alpha}{4\pi} \times 10^{-4}$ (using $\lambda$ in microns and $\alpha$ in cm⁻¹)

An important consideration is that Tidy3D uses microns (µm) as distance units, while $\alpha$ is generally given in cm⁻¹.

With the $k$ value, we can define a lossy medium using the td.Medium.from_nk method.

Let’s consider a medium with a real refractive index of 3 and $\alpha = 0.5$ $µ\text{m}^{-1}$.

Relating k with Conductivity¶

Alternatively, we can relate the complex refractive index with the complex permittivity and calculate the conductivity $\sigma$.

$\tilde{n} = n + i\kappa$

$\varepsilon_r = \tilde{n}^2 = (n^2 - \kappa^2) + i(2n\kappa)$

$\varepsilon'' = 2n\kappa$

$\sigma(\omega) = \omega \varepsilon_0 \varepsilon'' = 2\omega \varepsilon_0 n \kappa$

$\sigma(\omega) = \frac{4\pi \varepsilon_0 c}{\lambda} n \kappa$ [S/µm]

Again, following Tidy3D’s unit convention, the conductivity is in units of S/µm.

With the conductivity value, we can create the same medium using the regular td.Medium class.

As we can see, the two methods are equivalent.

Simulating the Beer-Lambert Law¶

With the lossy medium defined, we can use it as the background medium in a simulation and calculate the absorbed power using the following definition:

$P_{abs} = \tfrac{1}{2} \, \omega \, \varepsilon_0 \, \varepsilon'' \, |E|^2 = \tfrac{1}{2} \, \sigma \, |E|^2$

First, let’s define the simulation object.

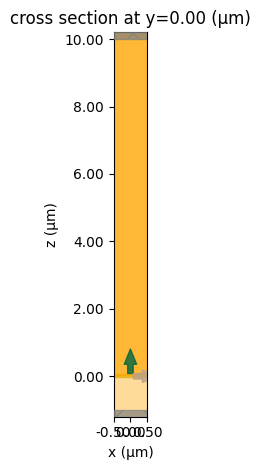
Now we can run the simulation and process the data.

Data Processing¶

First, let’s plot the fields, where we can observe an exponential decay in the field intensity.

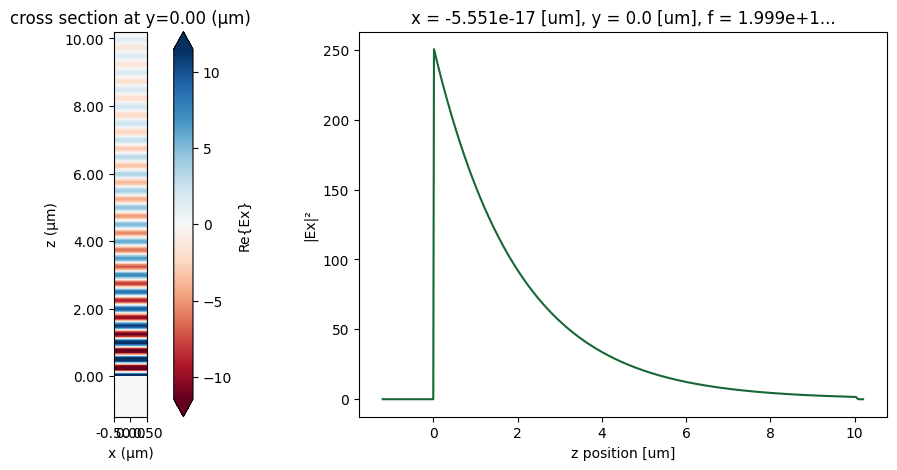
Now, we can calculate the volumetric absorbed power, using the following relation:

$P_{abs} = \tfrac{1}{2} \, \omega \, \varepsilon_0 \, \varepsilon'' \, |E|^2$

And compare with the analytical results, from Beer-Lambert law:

$I = I_0 e^{-\alpha z}$

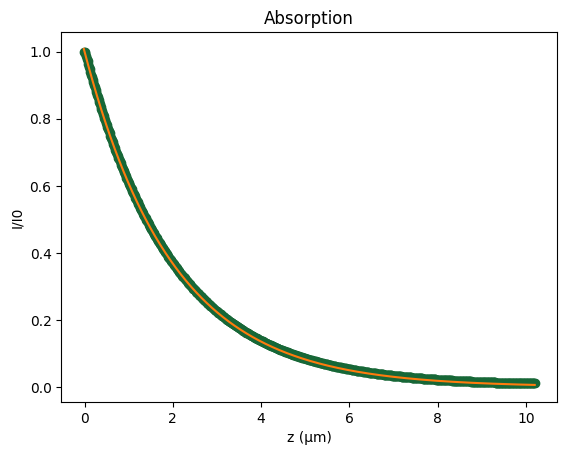
Finally, we compute the cumulative integral of the volumetric absorbed power along the full z-direction and directly compare the resulting energy loss with the analytical prediction given by the Beer–Lambert law.