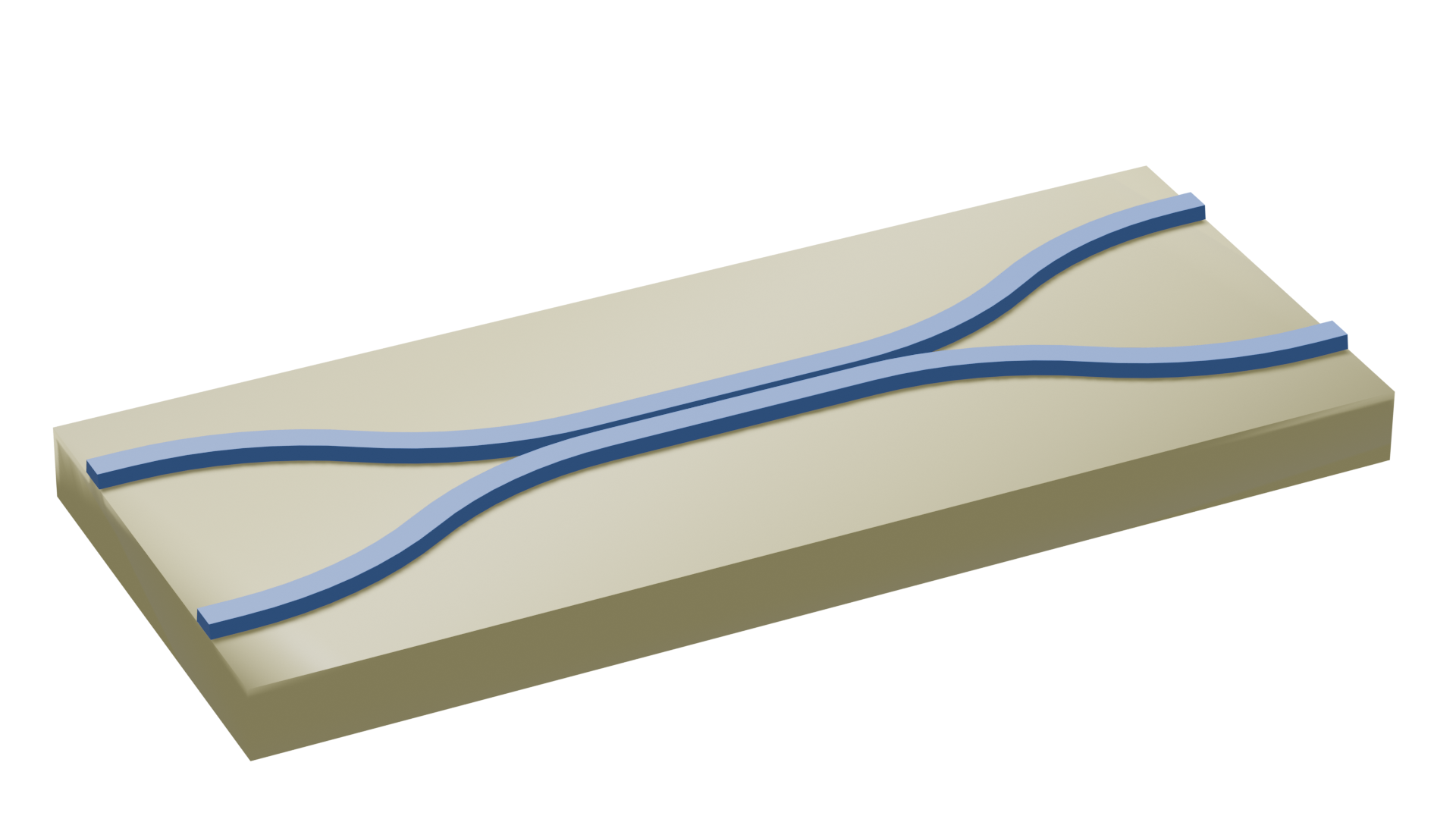
This notebook explores the design and simulation of a dielectric-to-plasmonic waveguide coupler using Tidy3D. Such couplers enable efficient transfer of optical signals from conventional silicon photonic waveguides to plasmonic waveguides, which support highly confined modes beyond the diffraction limit.
The coupler features a silicon strip waveguide that gradually tapers into a metallic slot waveguide. We utilize Bayesian optimization to systematically refine the design for maximum coupling efficiency.
![]()
import matplotlib.pyplot as plt
import numpy as np
import tidy3d as td
import tidy3d.web as web
Base Simulation Setup¶
Define central wavelength/frequency, a wavelength range, and its mapped frequency grid.
# define frequency and wavelength range
lda0 = 1.50
freq0 = td.C_0 / lda0
ldas = np.linspace(1.45, 1.55, 21)
freqs = td.C_0 / ldas
fwidth = 0.5 * (np.max(freqs) - np.min(freqs))
Load silicon, silica, and gold mediums from the built-in material library for the coupler stack.
si = td.material_library["cSi"]["Palik_Lossless"]
sio2 = td.material_library["SiO2"]["Palik_Lossless"]
au = td.material_library["Au"]["Olmon2012crystal"]
Set static geometric parameters such as the plasmonic slot length, silicon/gold layer thickness, slot width, and so on.
l_slot = 1.5 # plasmonic waveguide length
h = 0.25 # both silicon and gold layer thicknesses are 250 nm
w_slot = 0.2 # metal slot width
w_si = 0.45 # silicon waveguide width
inf_eff = 1e2 # effective infinity
buffer = 0.6 * lda0 # buffer spacing to pad the simulation domain
To streamline the design optimization process, we define a function make_sim() which accepts tunable design parameters including the taper angle, taper tip width, and gap size, and constructs a corresponding Tidy3D Simulation object.
# define the oxide layer
box = td.Structure(
geometry=td.Box.from_bounds(rmin=(-inf_eff, -inf_eff, -inf_eff), rmax=(inf_eff, inf_eff, 0)),
medium=sio2,
)
# add a mode source for excitation
mode_spec = td.ModeSpec(num_modes=1, target_neff=3.47)
mode_source = td.ModeSource(
center=(-0.9 * buffer, 0, h / 2),
size=(0, 4 * w_si, 6 * h),
source_time=td.GaussianPulse(freq0=freq0, fwidth=fwidth),
mode_spec=mode_spec,
mode_index=0,
direction="+",
num_freqs=1,
)
# add a field monitor to visualize the field distribution
field_monitor = td.FieldMonitor(
center=(0, 0, h / 2), size=(td.inf, td.inf, 0), freqs=[freq0], name="field"
)
# extrusion arguments for polyslab
polyslab_args = dict(axis=2, slab_bounds=(0, h))
# function to create a simulation given the design parameters
def make_sim(theta, d_tip, l_gap):
# calculate the taper length
l_taper = (w_si - d_tip) / (2 * np.tan(theta))
# define the input waveguide structure
vertices = [
(-inf_eff, -w_si / 2),
(0, -w_si / 2),
(l_taper, -d_tip / 2),
(l_taper, d_tip / 2),
(0, w_si / 2),
(-inf_eff, w_si / 2),
]
wg_in = td.Structure(geometry=td.PolySlab(vertices=vertices, **polyslab_args), medium=si)
# define the output waveguide structure
vertices = [
(l_taper + 2 * l_gap + l_slot, d_tip / 2),
(2 * l_taper + 2 * l_gap + l_slot, w_si / 2),
(inf_eff, w_si / 2),
(inf_eff, -w_si / 2),
(2 * l_taper + 2 * l_gap + l_slot, -w_si / 2),
(l_taper + 2 * l_gap + l_slot, -d_tip / 2),
]
wg_out = td.Structure(geometry=td.PolySlab(vertices=vertices, **polyslab_args), medium=si)
# define the top plasmonic waveguide
vertices = [
(l_taper + l_gap, w_slot / 2),
(l_taper + l_gap + l_slot, w_slot / 2),
(inf_eff, np.tan(theta) * inf_eff),
(-inf_eff, np.tan(theta) * inf_eff),
]
gold_top = td.Structure(geometry=td.PolySlab(vertices=vertices, **polyslab_args), medium=au)
# define the bottom plasmonic waveguide
vertices = [
(l_taper + l_gap, -w_slot / 2),
(l_taper + l_gap + l_slot, -w_slot / 2),
(inf_eff, -np.tan(theta) * inf_eff),
(-inf_eff, -np.tan(theta) * inf_eff),
]
gold_bottom = td.Structure(geometry=td.PolySlab(vertices=vertices, **polyslab_args), medium=au)
# add a mode monitor to measure transmission
mode_monitor = td.ModeMonitor(
center=(2 * l_taper + l_slot + 2 * l_gap + 0.9 * buffer, 0, h / 2),
size=mode_source.size,
freqs=freqs,
mode_spec=mode_spec,
name="mode",
)
# define simulation
sim = td.Simulation(
center=(l_taper + l_gap + l_slot / 2, 0, h / 2),
size=(2 * l_taper + 2 * l_gap + l_slot + 2 * buffer, w_si + 2 * buffer, h + 2 * buffer),
grid_spec=td.GridSpec.auto(min_steps_per_wvl=20),
boundary_spec=td.BoundarySpec(
x=td.Boundary.absorber(num_layers=80),
y=td.Boundary.absorber(),
z=td.Boundary.pml(),
),
run_time=5e-13,
structures=[box, wg_in, wg_out, gold_top, gold_bottom],
sources=[mode_source],
monitors=[mode_monitor, field_monitor],
symmetry=(0, -1, 0),
)
return sim
Build a first design instance and render a top view at z = h/2 to confirm geometry, source, and monitor locations.
sim = make_sim(theta=np.deg2rad(20), d_tip=0.1, l_gap=0.2)
sim.plot(z=h / 2, monitor_alpha=0.1)
plt.show()
Submit the initial simulation to the cloud to generate fields and monitor data for the baseline geometry.
sim_data = web.run(sim, "test run")
21:11:22 Eastern Daylight Time Created task 'test run' with task_id 'fdve-ef0ea98f-26b9-4a2c-8b50-827a0a39c3e1' and task_type 'FDTD'.
View task using web UI at 'https://tidy3d.simulation.cloud/workbench?taskId =fdve-ef0ea98f-26b9-4a2c-8b50-827a0a39c3e1'.
Task folder: 'default'.
Output()
21:11:24 Eastern Daylight Time Maximum FlexCredit cost: 0.318. Minimum cost depends on task execution details. Use 'web.real_cost(task_id)' to get the billed FlexCredit cost after a simulation run.
21:11:25 Eastern Daylight Time status = success
Output()
21:11:26 Eastern Daylight Time loading simulation from simulation_data.hdf5
Plot the real part of Hz on the $xy$ plane to inspect coupling in the initial (non‑optimized) geometry.
sim_data.plot_field("field", "Hz", "real", vmax=0.3)
plt.show()
Bayesian Optimization¶
Define an objective function that computes the average broadband transmission power in the fundamental mode based on simulation results. This serves as the figure of merit to be maximized during optimization.
For reference, the initial (unoptimized) device achieves a mean broadband transmission of 12.8%.
def cal_transmission(sim_data):
amp = sim_data["mode"].amps.sel(mode_index=0, direction="+").values
T = np.abs(amp) ** 2
return np.mean(T)
print(f"Transmission = {1e2 * cal_transmission(sim_data):.2f}%")
Transmission = 12.83%
Configure tidy3d.plugins.design to maximize transmission by sweeping theta, d_tip, and l_gap within bounds using a UCB (upper confidence bound) acquisition function.
import tidy3d.plugins.design as tdd
# define optimization method
method = tdd.MethodBayOpt(
initial_iter=10,
n_iter=15,
acq_func="ucb",
kappa=0.3,
seed=1,
)
# define optimization parameters
parameters = [
tdd.ParameterFloat(name="theta", span=(np.deg2rad(5), np.deg2rad(20))),
tdd.ParameterFloat(name="d_tip", span=(0.05, 0.2)),
tdd.ParameterFloat(name="l_gap", span=(0.1, 0.3)),
]
# define a design space
design_space = tdd.DesignSpace(
method=method, parameters=parameters, task_name="bay_opt", path_dir="./data"
)
# run the design optimization
results = design_space.run(make_sim, cal_transmission, verbose=True)
21:11:29 Eastern Daylight Time Running 10 Simulations
21:11:58 Eastern Daylight Time Best Fit from Initial Solutions: 0.322
Running 1 Simulations
21:12:49 Eastern Daylight Time Latest Best Fit on Iter 0: 0.355
Running 1 Simulations
21:14:06 Eastern Daylight Time Latest Best Fit on Iter 1: 0.361
21:14:07 Eastern Daylight Time Running 1 Simulations
21:15:23 Eastern Daylight Time Running 1 Simulations
21:16:12 Eastern Daylight Time Latest Best Fit on Iter 3: 0.373
Running 1 Simulations
21:17:31 Eastern Daylight Time Latest Best Fit on Iter 4: 0.374
Running 1 Simulations
21:18:19 Eastern Daylight Time Latest Best Fit on Iter 5: 0.379
21:18:20 Eastern Daylight Time Running 1 Simulations
21:19:04 Eastern Daylight Time Latest Best Fit on Iter 6: 0.381
Running 1 Simulations
21:20:25 Eastern Daylight Time Latest Best Fit on Iter 7: 0.387
21:20:26 Eastern Daylight Time Running 1 Simulations
21:21:14 Eastern Daylight Time Latest Best Fit on Iter 8: 0.389
21:21:15 Eastern Daylight Time Running 1 Simulations
21:22:36 Eastern Daylight Time Latest Best Fit on Iter 9: 0.395
Running 1 Simulations
21:23:57 Eastern Daylight Time Running 1 Simulations
21:25:17 Eastern Daylight Time Latest Best Fit on Iter 11: 0.4
21:25:18 Eastern Daylight Time Running 1 Simulations
21:26:38 Eastern Daylight Time Running 1 Simulations
21:28:00 Eastern Daylight Time Latest Best Fit on Iter 13: 0.401
Running 1 Simulations
21:29:22 Eastern Daylight Time Latest Best Fit on Iter 14: 0.401
Best Result: 0.401350274778198 Best Parameters: d_tip: 0.13292462551997172 l_gap: 0.1 theta: 0.08726646259971647
Rebuild the simulation with the best parameters from optimization.
sim_opt = make_sim(**results.optimizer.max["params"])
sim_opt.plot(z=h / 2, monitor_alpha=0.2)
plt.show()
Run the optimized simulation (cached) again and plot the real part of Hz on the $xy$ plane to confirm efficient coupling into the slot plasmonic mode.
sim_data_opt = web.run(sim_opt, "optimal design")
sim_data_opt.plot_field("field", "Hz", "real", vmax=0.5)
plt.show()
21:29:23 Eastern Daylight Time Created task 'optimal design' with task_id 'fdve-33c63420-9e17-4c9c-b46a-929b1a526b2a' and task_type 'FDTD'.
View task using web UI at 'https://tidy3d.simulation.cloud/workbench?taskId =fdve-33c63420-9e17-4c9c-b46a-929b1a526b2a'.
Task folder: 'default'.
Output()
21:29:24 Eastern Daylight Time Maximum FlexCredit cost: 0.448. Minimum cost depends on task execution details. Use 'web.real_cost(task_id)' to get the billed FlexCredit cost after a simulation run.
21:29:25 Eastern Daylight Time status = success
Output()
21:29:26 Eastern Daylight Time loading simulation from simulation_data.hdf5
Finally, compute and plot power transmission from the mode monitor across the wavelength range.
amp = sim_data_opt["mode"].amps.sel(mode_index=0, direction="+")
T = np.abs(amp) ** 2
plt.plot(ldas, T, c="red", linewidth=2)
plt.xlabel("Wavelength (μm)")
plt.ylabel("Transmission")
plt.ylim(0, 1)
plt.grid()
plt.show()