TIDY3D
LEARNING CENTER

Lectures

Tutorials

Applications

Quickstart¶

This is a minimal Tidy3D script showing the FDTD simulation of a dielectric cube in the presence of a point dipole.

Before running this notebook, make sure to have:

[1]:

# import packages and authenticate (if needed)
import matplotlib.pylab as plt
import numpy as np
import tidy3d as td
import tidy3d.web as web

# web.configure("YOUR API KEY GOES HERE")

[2]:

lda0 = 0.75  # wavelength of interest (length scales are micrometers in Tidy3D)
freq0 = td.C_0 / lda0  # frequency of interest

Create a Structure from a Geometry like this rectangular prism Box and assign a Medium to represent its optical properties.

[3]:

square = td.Structure(
    geometry=td.Box(center=(0, 0, 0), size=(1.5, 1.5, 1.5)), medium=td.Medium(permittivity=2.0)
)

Create a Source. In this case, it is a PointDipole, which is a uniform current source with a zero size.

[4]:

# create source
source = td.PointDipole(
    center=(-1.5, 0, 0),  # position of the dipole
    source_time=td.GaussianPulse(freq0=freq0, fwidth=freq0 / 10.0),  # time profile of the source
    polarization="Ey",  # polarization of the dipole
)

Create a Monitor like a FieldMonitor to record electromagnetic fields in the frequency domain at freq0.

[5]:

# create monitor
monitor = td.FieldMonitor(
    center=(0, 0, 0),  # center of the monitor
    size=(td.inf, td.inf, 0),  # size of the monitor
    freqs=[freq0],  # frequency points to record the fields at
    name="fields",
)

All these components are used to create a Tidy3D Simulation:

[6]:

sim = td.Simulation(
    size=(4, 3, 3),  # simulation domain size
    grid_spec=td.GridSpec.auto(
        min_steps_per_wvl=25
    ),  # automatic nonuniform FDTD grid with 25 grids per wavelength in the material
    structures=[square],
    sources=[source],
    monitors=[monitor],
    run_time=3e-13,  # physical simulation time in second
)

[7]:

# visualize in 3D
sim.plot_3d()

[8]:

print(
    f"simulation grid is shaped {sim.grid.num_cells} for {int(np.prod(sim.grid.num_cells) / 1e6)} million cells."
)

simulation grid is shaped [179, 147, 147] for 3 million cells.

The python web API is used to run your simulation quickly in the cloud. The output data is stored in a SimulationData container.

[9]:

# run simulation
data = td.web.run(sim, task_name="quickstart", path="data/data.hdf5", verbose=True)

13:39:37 CEST Created task 'quickstart' with task_id                            
              'fdve-68b6eaf9-2237-470c-a4a1-4940fbc8c910' and task_type 'FDTD'.

              View task using web UI at                                         
              'https://tidy3d.simulation.cloud/workbench?taskId=fdve-68b6eaf9-22
              37-470c-a4a1-4940fbc8c910'.

              Task folder: 'default'.

Output()

13:39:39 CEST Maximum FlexCredit cost: 0.025. Minimum cost depends on task      
              execution details. Use 'web.real_cost(task_id)' to get the billed 
              FlexCredit cost after a simulation run.

13:39:40 CEST status = success

Output()

13:39:44 CEST loading simulation from data/data.hdf5

[10]:

# see the log
print(data.log)

[10:27:22] INFO: Auto meshing using wavelength 0.7500 defined from sources.     
           INFO: Auto meshing using wavelength 0.7500 defined from sources.     
           USER: Simulation domain Nx, Ny, Nz: [179, 147, 147]                  
           USER: Applied symmetries: (0, 0, 0)                                  
           USER: Number of computational grid points: 4.0184e+06.               
           USER: Subpixel averaging method: SubpixelSpec(attrs={},              
           dielectric=PolarizedAveraging(attrs={}, type='PolarizedAveraging'),  
           metal=Staircasing(attrs={}, type='Staircasing'),                     
           pec=PECConformal(attrs={}, type='PECConformal',                      
           timestep_reduction=0.3), lossy_metal=SurfaceImpedance(attrs={},      
           type='SurfaceImpedance', timestep_reduction=0.0),                    
           type='SubpixelSpec')                                                 
           USER: Number of time steps: 7.5090e+03                               
           USER: Automatic shutoff factor: 1.00e-05                             
           USER: Time step (s): 3.9959e-17                                      
           USER:                                                                
                                                                                
           USER: Compute source modes time (s):     0.0486                      
[10:27:23] USER: Rest of setup time (s):            0.3159                      
[10:27:28] USER: Compute monitor modes time (s):    0.0001                      
[10:27:35] USER: Solver time (s):                   1.2020                      
           USER: Time-stepping speed (cells/s):     8.77e+09                    
           USER: Post-processing time (s):          0.1622                      

 ====== SOLVER LOG ====== 

Processing grid and structures...
Building FDTD update coefficients...
Solver setup time (s):             0.4730

Running solver for 7509 time steps...
- Time step    300 / time 1.20e-14s (  4 % done), field decay: 1.00e+00
- Time step    498 / time 1.99e-14s (  6 % done), field decay: 1.00e+00
- Time step    600 / time 2.40e-14s (  8 % done), field decay: 3.00e-01
- Time step    901 / time 3.60e-14s ( 12 % done), field decay: 2.62e-03
- Time step   1201 / time 4.80e-14s ( 16 % done), field decay: 6.44e-05
- Time step   1501 / time 6.00e-14s ( 20 % done), field decay: 2.26e-06
Field decay smaller than shutoff factor, exiting solver.
Time-stepping time (s):            0.6881
Data write time (s):               0.0103

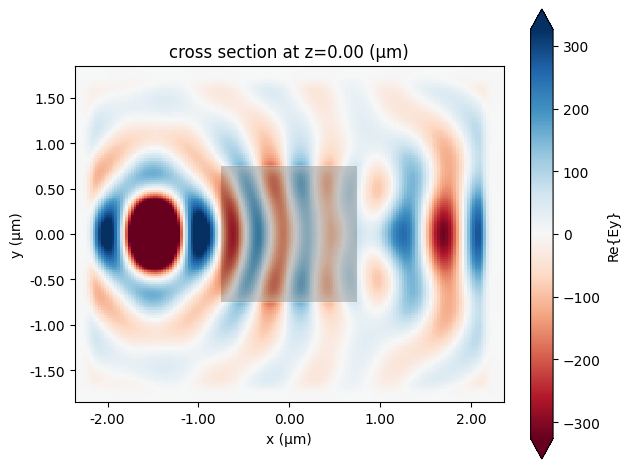
This monitor data can be easily plotted through available plot methods. You can also save, modify, and custom plot the raw FieldData and more.

[11]:

# plot the field data stored in the monitor
ax = data.plot_field("fields", "Ey", z=0)

No description has been provided for this image

See all our examples to help you with your own designs!

[ ]:

Example library

Next Tutorial

TIDY3D LEARNING CENTER

Quickstart¶

TIDY3D
LEARNING CENTER