Author: Amberly Xie, Harvard University
1D photonic crystal cavities enhance light-matter interaction for point defects, improving zero phonon line emission, which is essential for many quantum applications involving solid-state point defects. This notebook contains code for designing 1D photonic crystal cavities in 4H-SiC.
First, we will perform a band structure calculation to examine the photonic band gap. Next, we will simulate the full cavity and use the ResonanceFinder plugin to obtain the resonance frequency and quality factor.
The cavity consists of two stacks of unit cells with the photonic band gap tuned to the desired resonance frequency, and a tapered region where the unit cell parameters are gradually modified to confine the resonance mode.
Importing Packages and Defining Useful Functions¶
[1]:
import matplotlib.pyplot as plt
import numpy as np
import tidy3d as td
from tidy3d import web
from tidy3d.plugins.resonance import ResonanceFinder
[2]:
# --- Function for filtering resonances ---
def filter_resonances(resonance_data, minQ, minamp, maxerr):
resonance_data = resonance_data.where(abs(resonance_data.Q) > minQ, drop=True)
resonance_data = resonance_data.where(resonance_data.amplitude > minamp, drop=True)
resonance_data = resonance_data.where(resonance_data.error < maxerr, drop=True)
resonance_data = resonance_data.where(resonance_data.freq > 0, drop=True)
return resonance_data
[3]:
# --- Function to convert from freq to nm ---
def freq_nm(freq):
return (td.C_0 / freq) * 1e3
[4]:
# --- Function to find the cavity mode ---
def cavitymode(resonance_data):
freq = resonance_data.freq
nm = freq_nm(freq)
Q = resonance_data.Q
amplitude = resonance_data.amplitude
cost = (amplitude * Q) / (np.pi * nm)
idx = cost.argmax()
return float(freq[idx]), float(Q[idx])
[5]:
# --- Function to calculate mode volume ---
def findvmode(sim, data, field_mnt, eps_mnt, freq0):
# Get grid points
xaxis = np.array(data[eps_mnt].eps_xx.x)
yaxis = np.array(data[eps_mnt].eps_xx.y)
zaxis = np.array(data[eps_mnt].eps_xx.z)
# Get E-field data
Ex = np.array(data[field_mnt].Ex).squeeze()
Ey = np.array(data[field_mnt].Ey).squeeze()
Ez = np.array(data[field_mnt].Ez).squeeze()
E_sqr = np.abs(Ex) ** 2 + np.abs(Ey) ** 2 + np.abs(Ez) ** 2
E_sqr_pad = np.pad(E_sqr, ((0, 1), (0, 1), (0, 1)), "constant")
eps = (np.array(data[eps_mnt].eps_xx).squeeze()).real
# Calculate mode volume
vmode = (
np.trapz(
np.trapz(np.trapz(eps * E_sqr_pad, xaxis, axis=0), yaxis, axis=0),
zaxis,
axis=0,
)
) / (np.max(eps * E_sqr_pad))
n_sic = 2.59
# Normalize mode volume
wv = freq_nm(freq0) * 1e-3
vmode = vmode / ((wv / n_sic) ** 3)
return vmode
Simulating Mirror Cells¶
We begin by simulating the band structure for the mirror cells, targeting a bandgap centered around surface state emission (700nm).
[6]:
# --- Simulation parameters ---
epAir = 1
epSic = 2.6**2
# Frequency range of interest
ss1 = td.C_0 / (400e-3)
ss2 = td.C_0 / (1000e-3)
ss0 = td.C_0 / (700e-3)
ssWidth = 149999999997498 / 2.35
# Runtime
runtime = 800 / ssWidth
tstart = 5 / ssWidth
Building the Simulation¶
[7]:
# --- Function for creating ellipse unit cells ---
def ellipse_uc(center, x_axis, y_axis, height=0.5):
theta = np.linspace(0, np.pi * 2, 1001)
x = x_axis * np.cos(theta) + center[0]
y = y_axis * np.sin(theta) + center[1]
geometry = td.PolySlab(
vertices=np.array([x, y]).T,
slab_bounds=(-height / 2 + center[2], height / 2 + center[2]),
axis=2,
)
return geometry
[8]:
# --- Setting up simulation ---
def makecells(params):
a = params[0] # Lattice constant
a1 = params[1] # X width of holes
a2 = params[2] # Y width of holes
w = params[3] # Width of beam
h = 0.3 # Thickness
matSlab = td.Medium(permittivity=epSic, name="matSlab")
matHole = td.Medium(permittivity=epAir, name="matHole")
slab = td.Structure(
geometry=td.Box(
center=(0, 0, 0),
size=(td.inf, w, h),
),
medium=matSlab,
name="slab",
)
hole = td.Structure(
geometry=ellipse_uc((0, 0, 0), a1, a2, height=0.5), medium=matHole, name="hole"
)
structures = [slab, hole]
# Sources and monitors
numDipoles = 5
numMonitors = 2
polarization = "Ey"
rng = np.random.default_rng(12345)
dipolePos = rng.uniform([-a / 2, -w / 2, 0], [a / 2, w / 2, 0], [numDipoles, 3])
monitorPos = rng.uniform([-a / 2, -w / 2, 0], [a / 2, w / 2, 0], [numDipoles, 3])
dipolePhase = rng.uniform(0, 2 * np.pi, numDipoles)
pulses = []
dipoles = []
for i in range(numDipoles):
pulse = td.GaussianPulse(freq0=ss0, fwidth=ssWidth, phase=dipolePhase[i])
pulses.append(pulse)
dipoles.append(
td.PointDipole(
source_time=pulse,
center=tuple(dipolePos[i]),
polarization=polarization,
name="dipole-" + str(i),
)
)
monitorsTime = []
for i in range(numMonitors):
monitorsTime.append(
td.FieldTimeMonitor(
fields=["Ey"],
center=tuple(monitorPos[i]),
size=(0, 0, 0),
start=tstart,
name="monitor-time-" + str(i),
)
)
# Boundary conditions
bspecs = td.BoundarySpec(
x=td.Boundary.bloch(0.5), y=td.Boundary.pml(), z=td.Boundary.pml()
)
simSize = (a, 2, 4)
return [structures, dipoles, monitorsTime, simSize, bspecs]
Running the Simulation¶
[9]:
params = [0.198, 0.066, 0.066, 0.345]
structures = makecells(params)[0]
dipoles = makecells(params)[1]
monitorsTime = makecells(params)[2]
simSize = makecells(params)[3]
bspecs = makecells(params)[4]
symmetry = (0, 0, 1)
sim = td.Simulation(
center=(0, 0, 0),
size=simSize,
grid_spec=td.GridSpec.auto(),
structures=structures,
sources=dipoles,
monitors=monitorsTime,
run_time=runtime,
shutoff=0,
boundary_spec=bspecs,
normalize_index=None,
symmetry=symmetry,
)
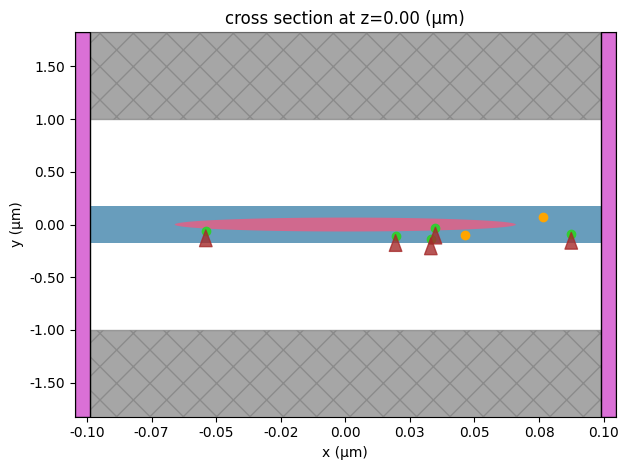
ax = sim.plot(z=0)
ax.set_aspect('auto')
plt.show()
[10]:
# Upload task
task_id = web.upload(sim, task_name="NBBands")
# Run simulation
NBBandsData = web.run(
sim, "NBBands", folder_name="data", path="data/NBBands.hdf5", verbose=True
)
19:27:09 -03 Created task 'NBBands' with task_id 'fdve-714413e5-9ab3-4e1b-b21e-9cfbda4c6aec' and task_type 'FDTD'.
View task using web UI at 'https://tidy3d.simulation.cloud/workbench?taskId=fdve-714413e5-9ab 3-4e1b-b21e-9cfbda4c6aec'.
Task folder: 'default'.
Output()
19:27:11 -03 Maximum FlexCredit cost: 0.025. Minimum cost depends on task execution details. Use 'web.real_cost(task_id)' to get the billed FlexCredit cost after a simulation run.
19:27:12 -03 Created task 'NBBands' with task_id 'fdve-39c3fdb4-03d8-4489-9d5a-87f048a66071' and task_type 'FDTD'.
View task using web UI at 'https://tidy3d.simulation.cloud/workbench?taskId=fdve-39c3fdb4-03d 8-4489-9d5a-87f048a66071'.
Task folder: 'data'.
Output()
19:27:14 -03 Maximum FlexCredit cost: 0.025. Minimum cost depends on task execution details. Use 'web.real_cost(task_id)' to get the billed FlexCredit cost after a simulation run.
19:27:15 -03 status = success
Output()
19:27:20 -03 loading simulation from data/NBBands.hdf5
[11]:
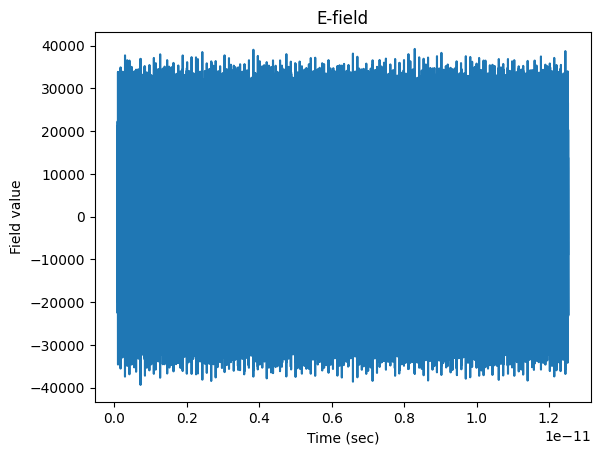
# Plotting E field as a function of time
plt.plot(
NBBandsData.monitor_data["monitor-time-0"].Ey.t,
np.real(NBBandsData.monitor_data["monitor-time-0"].Ey.squeeze()),
)
plt.xlabel("Time (sec)")
plt.ylabel("Field value")
plt.title("E-field")
plt.show()
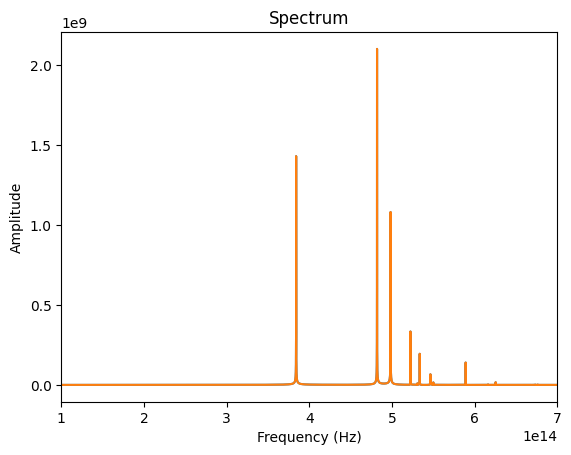
# Plot spectra
time_series = np.real(NBBandsData.monitor_data["monitor-time-0"].Ey.squeeze())
dt = NBBandsData.simulation.dt
fmesh = np.fft.fftshift(np.fft.fftfreq(time_series.size, dt))
spectrum = np.fft.fftshift(np.fft.fft(time_series))
plt.plot(fmesh, np.abs(spectrum))
time_series = np.real(NBBandsData.monitor_data["monitor-time-0"].Ey.squeeze())
dt = NBBandsData.simulation.dt
fmesh = np.fft.fftshift(np.fft.fftfreq(time_series.size, dt))
spectrum = np.fft.fftshift(np.fft.fft(time_series))
plt.plot(fmesh, np.abs(spectrum))
plt.xlim(1e14, 7e14)
plt.title("Spectrum")
plt.xlabel("Frequency (Hz)")
plt.ylabel("Amplitude")
plt.show()
# Run resonance finder
resonance_finder = ResonanceFinder(freq_window=tuple((ss2, ss1)))
resonance_data = resonance_finder.run(signals=NBBandsData.data)
# Filter resonances
resonance_data_filtered = filter_resonances(
resonance_data=resonance_data, minQ=100, minamp=0.001, maxerr=100
)
freqs = resonance_data_filtered.freq.to_numpy()
# Target frequency
v0 = 428274940000000
# Center frequency
v1 = None
v2 = None
for freq in freqs:
if freq < v0:
v1 = freq
elif freq > v0:
v2 = freq
break
# Calculating band edges
print(f"Wavelength 1: {freq_nm(v1):.2f}")
print(f"Wavelength 2: {freq_nm(v2):.2f}")
Wavelength 1: 780.46 Wavelength 2: 622.03
Simulating 1D Photonic Crystal Cavity¶
Building the Simulation¶
[12]:
# --- Set up structures ---
def makecells(params):
a = params[0] # Lattice constant
a1 = params[1] # X width
a2 = params[2] # Y width
w = params[3] # Width of beam
t = params[4] # Taper constant
nummirr = 12 # Number of mirror cells on each side
numtaper = 8 # Half the number of taper cells
h = 0.3 # Thickness
matSlab = td.Medium(permittivity=epSic, name="matSlab")
matHole = td.Medium(permittivity=epAir, name="matHole")
# Array to hold lattice constants
latticeconsttemp = []
a1temp = []
a2temp = []
# Adding mirror cell lattice constants
for i in np.arange(0, nummirr):
latticeconsttemp.append(a)
a1temp.append(a1)
a2temp.append(a2)
# Adding taper cell lattice constants
for i, num in enumerate(np.arange(0, numtaper)):
latticeconsttemp.append((t ** (i + 1)) * a)
a1temp.append((t ** (i + 1)) * a1)
a2temp.append((t ** (i + 1)) * a2)
latticeconstL = latticeconsttemp
latticeconstR = latticeconsttemp[::-1]
a1L = a1temp
a1R = a1temp[::-1]
a2L = a2temp
a2R = a2temp[::-1]
structures = []
slab = td.Structure(
geometry=td.Box(
center=(0, 0, 0),
size=(td.inf, w, h),
),
medium=matSlab,
name="slab",
)
structures.append(slab)
# Setting up nanobeam
for i, const in enumerate(latticeconstL):
center = (-np.sum(latticeconstL[i + 1 :]) - const / 2, 0, 0)
hole = td.Structure(
geometry=ellipse_uc(center, a1L[i], a2L[i], height=0.5),
medium=matHole,
name="holeL" + str(i),
)
structures.append(hole)
for i, const in enumerate(latticeconstR):
center = (np.sum(latticeconstR[:i]) + const / 2, 0, 0)
hole = td.Structure(
geometry=ellipse_uc(center, a1R[i], a2R[i], height=0.5),
medium=matHole,
name="holeR" + str(i),
)
structures.append(hole)
# Set up sources and monitors
source = td.PointDipole(
center=(0, 0, 0),
source_time=td.GaussianPulse(freq0=ss0, fwidth=ssWidth),
polarization="Ey",
)
point_t_mnt = td.FieldTimeMonitor(
center=[0, 0, 0],
size=[0, 0, 0],
start=tstart,
name="point",
colocate=True, # Colocate so field is colocated to grid cell centers
)
field_t_mnt = td.FieldTimeMonitor(
center=[0, 0, 0],
size=[td.inf, td.inf, td.inf],
start=runtime,
name="field",
colocate=True,
)
eps_mnt = td.PermittivityMonitor(
center=[0, 0, 0], size=[td.inf, td.inf, td.inf], freqs=[ss0], name="eps"
)
# Boundary conditions
bspecs = td.BoundarySpec(
x=td.Boundary.pml(), y=td.Boundary.pml(), z=td.Boundary.pml()
)
simSize = (a * 2 * len(latticeconstL) * 1.1, w * 5, 1.5)
return structures, simSize, bspecs, source, point_t_mnt, field_t_mnt, eps_mnt
Running the simulation¶
[13]:
params = [0.198, 0.066, 0.066, 0.345, 0.97]
simsetup = makecells(params)
structures = simsetup[0]
simSize = simsetup[1]
bspecs = simsetup[2]
source = simsetup[3]
point_t_mnt = simsetup[4]
field_t_mnt = simsetup[5]
eps_mnt = simsetup[6]
symmetry = (1, -1, 1)
mesh_override = td.MeshOverrideStructure(
geometry=td.Box(center=(0, 0, 0), size=(0.5, 0.5, 0.5 * 1.5)), dl=[0.01, 0.01, 0.01]
)
# Define grid specification for the simulation
grid_spec = td.GridSpec.auto(
min_steps_per_wvl=10,
override_structures=[mesh_override],
)
sim = td.Simulation(
center=(0, 0, 0),
size=simSize,
grid_spec=td.GridSpec.auto(),
structures=structures,
sources=[source],
monitors=[point_t_mnt, field_t_mnt, eps_mnt],
run_time=runtime,
shutoff=0,
boundary_spec=bspecs,
normalize_index=None,
symmetry=symmetry,
)
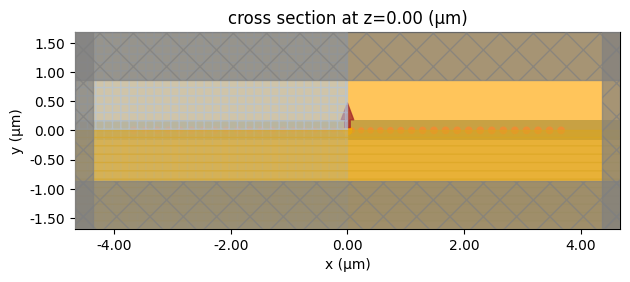
sim.plot(z=0)
plt.show()
[14]:
# Upload task
task_id = web.upload(sim, task_name="NBSym")
# Run simulation
NBSymData = web.run(
sim, "NBSym", folder_name="data", path="data/NBSym.hdf5", verbose=True
)
19:27:26 -03 Created task 'NBSym' with task_id 'fdve-ae84644a-fca1-4bf1-bf7d-79fbd39866d0' and task_type 'FDTD'.
View task using web UI at 'https://tidy3d.simulation.cloud/workbench?taskId=fdve-ae84644a-fca 1-4bf1-bf7d-79fbd39866d0'.
Task folder: 'default'.
Output()
19:27:31 -03 Maximum FlexCredit cost: 0.039. Minimum cost depends on task execution details. Use 'web.real_cost(task_id)' to get the billed FlexCredit cost after a simulation run.
Created task 'NBSym' with task_id 'fdve-db6b6c3d-0e5e-4416-80e8-78dd138b7a72' and task_type 'FDTD'.
View task using web UI at 'https://tidy3d.simulation.cloud/workbench?taskId=fdve-db6b6c3d-0e5 e-4416-80e8-78dd138b7a72'.
Task folder: 'data'.
Output()
19:27:36 -03 Maximum FlexCredit cost: 0.039. Minimum cost depends on task execution details. Use 'web.real_cost(task_id)' to get the billed FlexCredit cost after a simulation run.
19:27:37 -03 status = success
Output()
19:27:49 -03 loading simulation from data/NBSym.hdf5
[15]:
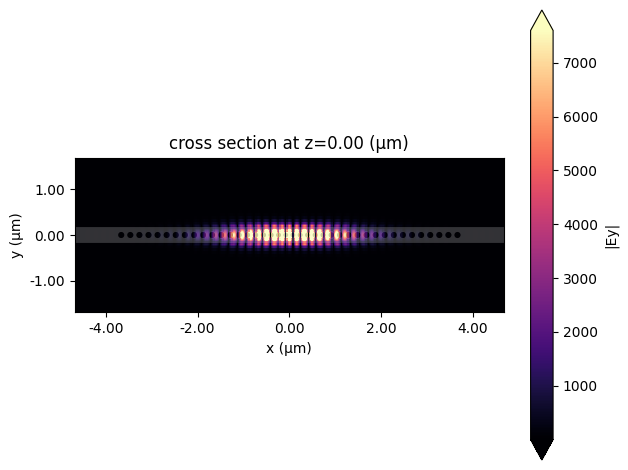
# Plotting E field at very end of simulation
final_time = NBSymData["field"].Ey.t
NBSymData.plot_field("field", "Ey", val="abs", t=final_time, z=0)
plt.show()
[16]:
# Get y-component of E field from point monitor
time_series = NBSymData["point"].Ey.squeeze()
# Run resonance finder
resonance_finder = ResonanceFinder(freq_window=tuple((ss2, ss1)))
resonance_data = resonance_finder.run_scalar_field_time(time_series)
resonance_data_filtered = filter_resonances(
resonance_data=resonance_data, minQ=100, minamp=0.001, maxerr=100
)
# Cavity mode with highest Q from filtered resonances
freqcav, Q = cavitymode(resonance_data_filtered)
print(f"Resonance frequency: {freq_nm(freqcav):.2f} nm")
print(f"Quality Factor: {Q}")
Resonance frequency: 691.37 nm Quality Factor: 3769908.6786274584
TERMS & CONDITIONS
How the process works:
Try this real URL to see an example: