Note: this notebook is 90% AI-generated.
In this notebook, we will design and simulate a 2x2 Multi-Mode Interference (MMI) power splitter for photonic integrated circuits (PICs). The MMI power splitter is a fundamental component in integrated photonics, providing equal power splitting (50/50) with high efficiency.
The design follows standard Silicon-on-Insulator (SOI) platform specifications with cosine S-bends for optimal performance. We will demonstrate the complete simulation workflow including geometry setup and performance evaluation.
For more integrated photonic examples such as the 8-Channel mode and polarization demultiplexer, the broadband bi-level taper polarization rotator-splitter, and the broadband directional coupler, please visit our examples page.
If you are new to the finite-difference time-domain (FDTD) method, we highly recommend going through our FDTD101 tutorials.
FDTD simulations can diverge due to various reasons. If you run into any simulation divergence issues, please follow the steps outlined in our troubleshooting guide to resolve it.
Standard Python Imports¶
We start by importing the necessary libraries for our simulation.
# Standard python imports.
import gdstk
import matplotlib.pylab as plt
import numpy as np
# Import regular tidy3d.
import tidy3d as td
import tidy3d.web as web
MMI Power Splitter Structure¶
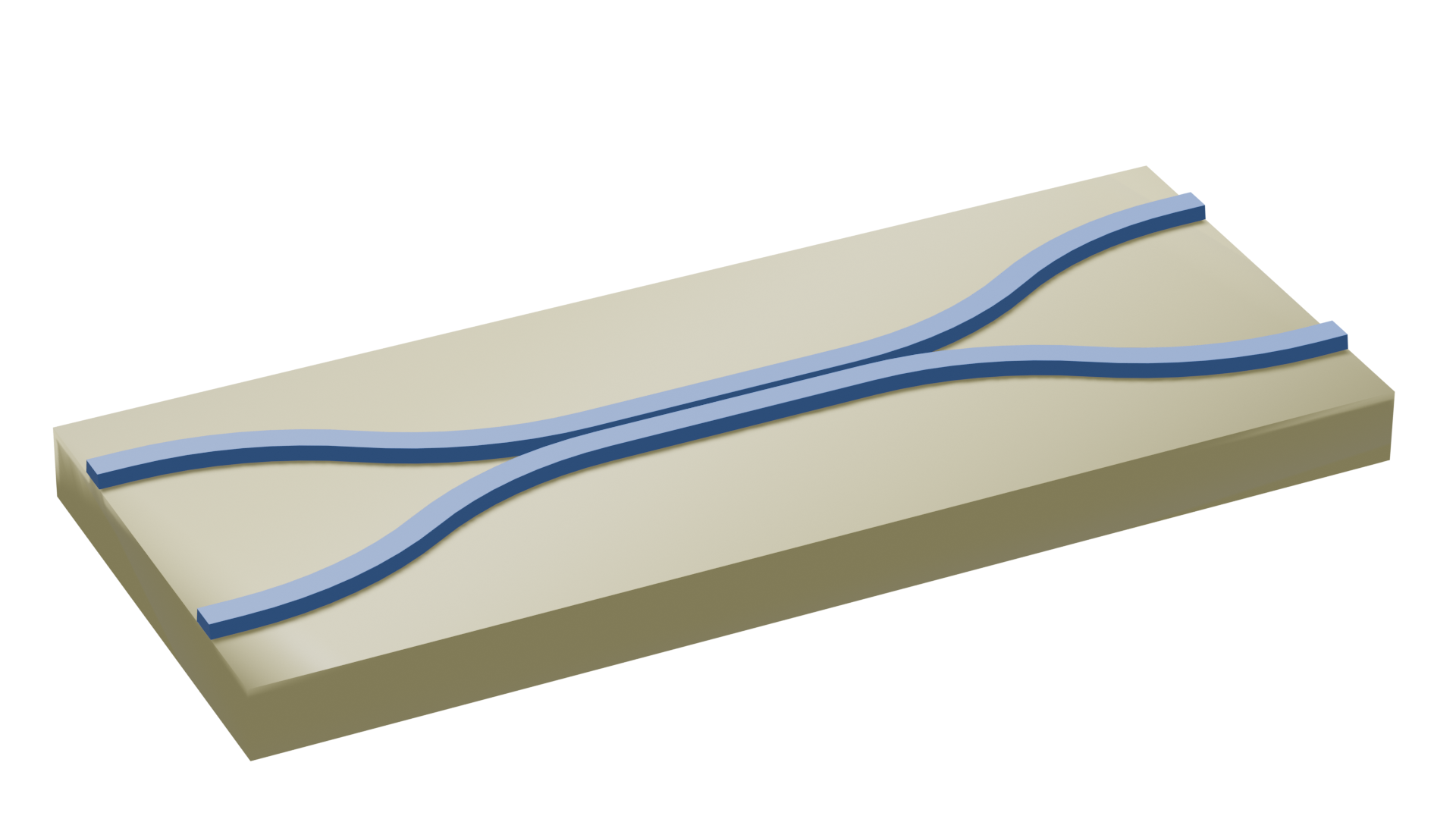
The 2x2 MMI power splitter is based on a standard Silicon-on-Insulator (SOI) wafer with a device layer of 220 nm. The MMI section provides multimode interference for equal power splitting, while cosine S-bends route the input/output signals to offset positions for practical device integration.
Key Design Parameters:
- Material Platform: Silicon-on-Insulator (SOI)
- Wavelength Range: 1.5 to 1.6 μm (telecom C-band)
- Design Goal: Equal power splitting (50/50)
The MMI length is designed to achieve optimal interference patterns for equal power splitting around 1.55 micrometers, while the S-bends provide smooth transitions to offset input/output waveguides.
# MMI power splitter setup.
wavelength = 1.55 # Center simulation wavelength (um).
freq0 = td.C_0 / wavelength # Central frequency.
# Materials.
n_si = 3.48 # Silicon refractive index.
n_sio2 = 1.44 # SiO2 refractive index.
# Material definitions.
mat_si = td.Medium(permittivity=n_si**2) # Silicon waveguide material.
mat_sio2 = td.Medium(permittivity=n_sio2**2) # SiO2 substrate material.
# This cell contains all the geometry, sources, monitors, and simulation creation
# MMI power splitter dimensions.
w_wg = 0.4 # Waveguide width (um).
h_si = 0.22 # Silicon layer height (um).
w_mmi = 1.0 # MMI section width (um).
l_mmi = 3.0 # MMI section length (um).
gap = 0.2 # Gap between output waveguides (um).
# Waveguide lengths.
l_input = 2.0 # Input waveguide length (um).
l_output = 3.0 # Output waveguide length (um).
# S-bend parameters.
s_bend_offset = 1.0 # Lateral offset for S-bends (um).
s_bend_length = 4.0 # Length of S-bend section (um).
Cosine S-bend Function¶
We define a cosine S-bend function for smooth waveguide transitions. This function creates high-quality S-bends that minimize insertion loss.
# Function to create cosine S-bends.
def cosine_sbend(
x0,
y0,
z0,
wg_width,
wg_thickness,
bend_length,
bend_height,
medium,
orientation="x",
mirror=False,
sidewall_angle=0,
):
"""Cosine S-bend function for smooth waveguide transitions."""
cell = gdstk.Cell("bend")
path = gdstk.RobustPath((x0, y0), wg_width, layer=1, datatype=0)
if orientation == "x":
path.segment(
(x0 + bend_length, y0),
offset=lambda u: -bend_height * np.cos(np.pi * u) / 2 + bend_height / 2,
)
if mirror:
path.mirror((x0 + 1, y0), (x0, y0))
elif orientation == "y":
path.segment(
(x0, y0 + bend_length),
offset=lambda u: -bend_height * np.cos(np.pi * u) / 2 + bend_height / 2,
)
if mirror:
path.mirror((x0, y0 + 1), (x0, y0))
cell.add(path)
bend_geo = td.PolySlab.from_gds(
cell,
gds_layer=1,
axis=2,
slab_bounds=(z0 - wg_thickness / 2, z0 + wg_thickness / 2),
sidewall_angle=sidewall_angle,
)
return td.Structure(geometry=bend_geo[0], medium=medium)
Complete MMI Power Splitter Simulation Setup¶
Now we create the complete 2x2 MMI power splitter simulation with x-axis propagation. The simulation includes the MMI section, input/output waveguides, cosine S-bends, sources, and monitors.
# Calculate optimized simulation domain size for x-axis propagation.
x_min = -1.5 - 3.0 # -4.5 um
x_max = 5.5 + 3.0 # 8.5 um
total_length = x_max - x_min # 13.0 um
total_width = w_mmi + 4.0 # Keep width buffer for offset waveguides
total_height = 2.0 # Sufficient for SOI structure
sim_size_optimized = (total_length, total_width, total_height)
# 1. MMI section (main multimode interference region).
mmi_section = td.Structure(
geometry=td.Box(center=(0, 0, 0), size=(l_mmi, w_mmi, h_si)), medium=mat_si
)
# 2. Output S-bend 1.
output_s_bend_1 = cosine_sbend(
x0=l_mmi / 2, # Start at MMI right edge (x-axis propagation)
y0=w_wg / 2 + gap / 2, # Start at MMI top edge
z0=0,
wg_width=w_wg,
wg_thickness=h_si,
bend_length=s_bend_length,
bend_height=s_bend_offset,
medium=mat_si,
orientation="x",
mirror=False,
)
# 3. Output waveguide 1.
output_wg_1 = td.Structure(
geometry=td.Box(
center=(l_mmi / 2 + s_bend_length + l_output / 2, w_wg / 2 + gap / 2 + s_bend_offset, 0),
size=(l_output, w_wg, h_si),
),
medium=mat_si,
)
# 4. Output S-bend 2.
output_s_bend_2 = cosine_sbend(
x0=l_mmi / 2, # Start at MMI right edge (x-axis propagation)
y0=-w_wg / 2 - gap / 2, # Start at MMI bottom edge
z0=0,
wg_width=w_wg,
wg_thickness=h_si,
bend_length=s_bend_length,
bend_height=-s_bend_offset,
medium=mat_si,
orientation="x",
mirror=False,
)
# 5. Output waveguide 2.
output_wg_2 = td.Structure(
geometry=td.Box(
center=(l_mmi / 2 + s_bend_length + l_output / 2, -w_wg / 2 - gap / 2 - s_bend_offset, 0),
size=(l_output, w_wg, h_si),
),
medium=mat_si,
)
# 6. Create input waveguides using Tidy3D reflection transformation for x-axis propagation.
input_wg_1_geometry = output_wg_1.geometry.reflected(normal=(1, 0, 0))
input_wg_1 = td.Structure(geometry=input_wg_1_geometry, medium=mat_si)
input_wg_2_geometry = output_wg_2.geometry.reflected(normal=(1, 0, 0))
input_wg_2 = td.Structure(geometry=input_wg_2_geometry, medium=mat_si)
input_s_bend_1_geometry = output_s_bend_1.geometry.reflected(normal=(1, 0, 0))
input_s_bend_1 = td.Structure(geometry=input_s_bend_1_geometry, medium=mat_si)
input_s_bend_2_geometry = output_s_bend_2.geometry.reflected(normal=(1, 0, 0))
input_s_bend_2 = td.Structure(geometry=input_s_bend_2_geometry, medium=mat_si)
# 7. Combine all structures.
mmi_structures = [
input_s_bend_1,
input_wg_1,
input_s_bend_2,
input_wg_2,
mmi_section,
output_s_bend_1,
output_wg_1,
output_s_bend_2,
output_wg_2,
]
# 8. Create frequency array for wavelength sweep.
wavelengths = np.arange(1.5, 1.61, 0.01) # 1.5 to 1.6 μm with 10 nm steps
frequencies = td.C_0 / wavelengths
# 9. Mode source at the upper input waveguide (x-axis propagation).
source_position = (-6, 1.3, 0)
source_size = (0, 6 * w_wg, 6 * h_si)
mode_source = td.ModeSource(
center=source_position,
size=source_size,
source_time=td.GaussianPulse(freq0=freq0, fwidth=freq0 / 10),
direction="+",
mode_spec=td.ModeSpec(num_modes=1),
mode_index=0,
)
# 10. Mode monitors at the output waveguides (x-axis propagation).
monitor_1_position = (l_mmi / 2 + s_bend_length + 0.5, w_wg / 2 + gap / 2 + s_bend_offset, 0)
monitor_1_size = (0, 6 * w_wg, 6 * h_si)
mode_monitor_1 = td.ModeMonitor(
center=monitor_1_position,
size=monitor_1_size,
freqs=frequencies,
mode_spec=td.ModeSpec(num_modes=1),
name="mode_output_1",
)
monitor_2_position = (l_mmi / 2 + s_bend_length + 0.5, -w_wg / 2 - gap / 2 - s_bend_offset, 0)
monitor_2_size = (0, 6 * w_wg, 6 * h_si)
mode_monitor_2 = td.ModeMonitor(
center=monitor_2_position,
size=monitor_2_size,
freqs=frequencies,
mode_spec=td.ModeSpec(num_modes=1),
name="mode_output_2",
)
# 11. Field monitor at xy plane - record fields at specific wavelengths (x-axis propagation).
field_freqs = [td.C_0 / 1.55, td.C_0 / 1.58] # 1.55 and 1.58 um
field_monitor = td.FieldMonitor(
center=(0, 0, 0), size=(td.inf, td.inf, 0), freqs=field_freqs, name="field_xy"
)
# 12. Create the complete simulation.
sim_mmi = td.Simulation(
size=sim_size_optimized,
structures=mmi_structures,
sources=[mode_source],
monitors=[mode_monitor_1, mode_monitor_2, field_monitor],
run_time=1e-12,
boundary_spec=td.BoundarySpec.all_sides(boundary=td.PML()),
medium=mat_sio2,
grid_spec=td.GridSpec(
grid_x=td.AutoGrid(min_steps_per_wvl=20),
grid_y=td.AutoGrid(min_steps_per_wvl=20),
grid_z=td.AutoGrid(min_steps_per_wvl=20),
wavelength=wavelength,
),
symmetry=(0, 0, 0),
)
Simulation Visualization¶
Let's visualize the complete MMI power splitter setup to verify the geometry and propagation direction.
# Simulation Setup Visualization - XY Setup Plane
fig_xy = sim_mmi.plot(z=0) # XY cross-section at z=0 (MMI center) - shows complete setup
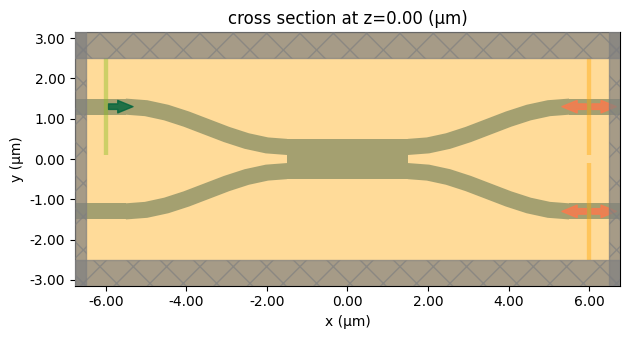
# 3D Visualization
fig_3d = sim_mmi.plot_3d()
Cost Estimation¶
Before running the simulation, let's estimate the computational cost.
# Cost Estimation
job = web.Job(simulation=sim_mmi, task_name="mmi_2x2_cost_estimation", verbose=True)
cost_info = web.estimate_cost(job.task_id)
print(f"Estimated cost: {cost_info:.4f} Flex Credits")
13:09:10 -03 Created task 'mmi_2x2_cost_estimation' with task_id 'fdve-4e41a63a-22fd-4da6-9504-1b43e0088728' and task_type 'FDTD'.
View task using web UI at 'https://tidy3d.simulation.cloud/workbench?taskId=fdve-4e41a63a-22f d-4da6-9504-1b43e0088728'.
Task folder: 'default'.
Output()
13:09:13 -03 Maximum FlexCredit cost: 0.077. Minimum cost depends on task execution details. Use 'web.real_cost(task_id)' to get the billed FlexCredit cost after a simulation run.
13:09:14 -03 Maximum FlexCredit cost: 0.077. Minimum cost depends on task execution details. Use 'web.real_cost(task_id)' to get the billed FlexCredit cost after a simulation run.
Estimated cost: 0.0774 Flex Credits
Run Simulation¶
Now we run the simulation to obtain the results.
# Run Simulation
sim_data = job.run(path="mmi_2x2_results.hdf5")
13:09:15 -03 status = success
Output()
13:09:19 -03 loading simulation from mmi_2x2_results.hdf5
Result Analysis¶
Let's analyze the simulation results to evaluate the MMI power splitter performance.
Key Performance Metrics:
-
Power Splitting Ratio: The fraction of total power that goes to each output port. For an ideal 2x2 MMI power splitter, both outputs should have a splitting ratio of 0.5 (50/50 split).
-
Total Power: The sum of power from both output ports, showing the overall transmission efficiency of the device.
# Extract mode coefficients from ModeMonitors
mode_coeff_1 = sim_data["mode_output_1"].amps.sel(mode_index=0, direction="+")
mode_coeff_2 = sim_data["mode_output_2"].amps.sel(mode_index=0, direction="+")
# Calculate power splitting
power_1 = np.abs(mode_coeff_1) ** 2
power_2 = np.abs(mode_coeff_2) ** 2
total_power = power_1 + power_2
# Calculate splitting ratio
splitting_ratio_1 = power_1 / total_power
splitting_ratio_2 = power_2 / total_power
# Ensure arrays are numpy arrays for consistent indexing
splitting_ratio_1 = np.array(splitting_ratio_1)
splitting_ratio_2 = np.array(splitting_ratio_2)
total_power = np.array(total_power)
# Create comprehensive analysis plots
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
# Power splitting vs wavelength
ax1.plot(wavelengths, splitting_ratio_1, "b-", label="Output 1", linewidth=2)
ax1.plot(wavelengths, splitting_ratio_2, "r-", label="Output 2", linewidth=2)
ax1.axhline(y=0.5, color="k", linestyle="--", alpha=0.7, label="Ideal 50/50")
ax1.set_xlabel("Wavelength (μm)")
ax1.set_ylabel("Power Splitting Ratio")
ax1.set_title("MMI Power Splitting vs Wavelength")
ax1.legend()
ax1.grid(True, alpha=0.3)
# Total power vs wavelength
ax2.plot(wavelengths, total_power, "g-", linewidth=2)
ax2.set_xlabel("Wavelength (μm)")
ax2.set_ylabel("Total Power")
ax2.set_title("Total Transmitted Power vs Wavelength")
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# Print key performance metrics
print(f"Average splitting ratio 1: {splitting_ratio_1.mean():.3f}")
print(f"Average splitting ratio 2: {splitting_ratio_2.mean():.3f}")
print(f"Average total power: {total_power.mean():.3f}")
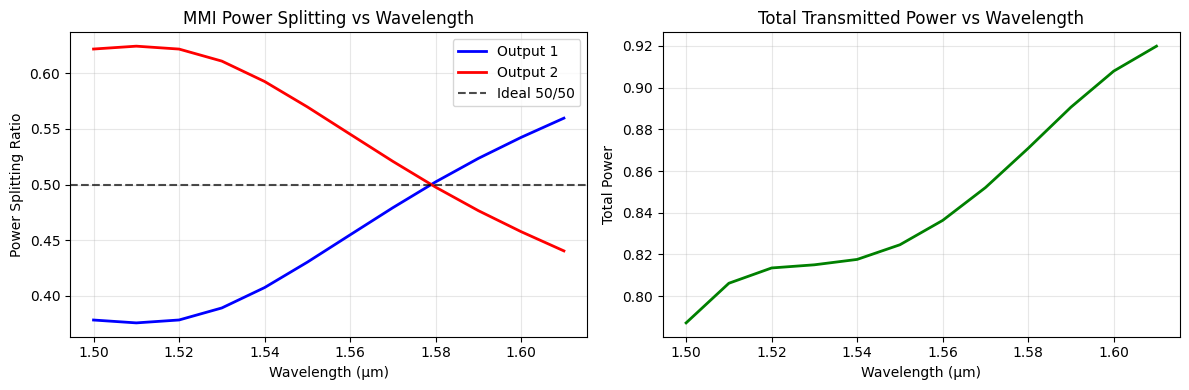
Average splitting ratio 1: 0.452 Average splitting ratio 2: 0.548 Average total power: 0.845
Power Splitting Performance Analysis:
The power splitting ratio plot reveals several important characteristics of the MMI power splitter:
-
Optimal Operating Wavelength: The device achieves perfect 50/50 splitting at approximately 1.58 μm, where both output curves intersect the ideal 50/50 line.
-
Wavelength Dependence: The splitting ratio shows significant wavelength dependence:
- At shorter wavelengths (1.50 μm): Output 2 receives ~62% of power, Output 1 receives ~37%
- At longer wavelengths (1.60 μm): Output 1 receives ~54% of power, Output 2 receives ~46%
-
Design Implications: This wavelength dependence is typical for MMI devices and can be optimized by adjusting the MMI length, width, or using apodization techniques for broader bandwidth performance.
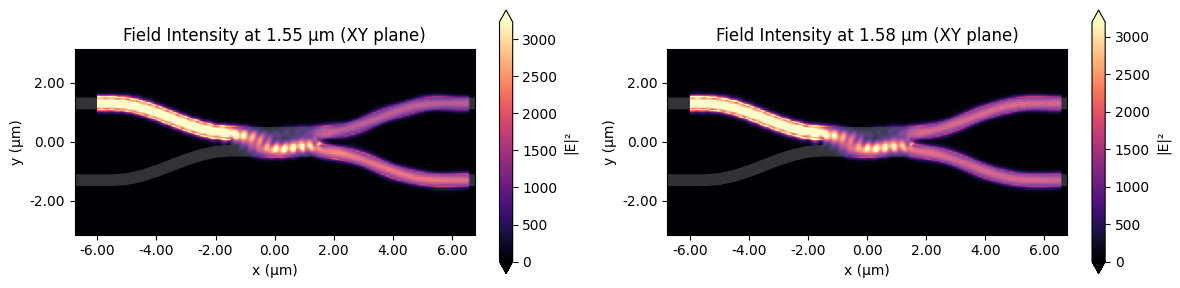
Field Intensity Analysis¶
Finally, let's examine the field intensity distribution at specific wavelengths in the XY plane to understand the light propagation through the MMI.
# Create a 2x1 subplot for the two wavelengths.
fig, axes = plt.subplots(1, 2, figsize=(12, 3))
# Plot field intensity at 1.55 um using Tidy3D's built-in method.
sim_data.plot_field("field_xy", "E", val="abs^2", f=td.C_0 / 1.55, ax=axes[0])
axes[0].set_title("Field Intensity at 1.55 μm (XY plane)")
# Plot field intensity at 1.58 um using Tidy3D's built-in method.
sim_data.plot_field("field_xy", "E", val="abs^2", f=td.C_0 / 1.58, ax=axes[1])
axes[1].set_title("Field Intensity at 1.58 μm (XY plane)")
plt.tight_layout()
plt.show()
TERMS & CONDITIONS
How the process works:
Try this real URL to see an example: