How Does Tidy3D’s Mode Solver Work?
Working Principles
A mode solver is a computational tool used to find the electromagnetic field distribution – or mode profile – and the propagation constant (β) of modes in a waveguide, optical fiber, or other types of guiding structures. To understand how a mode solver works, we consider a simple case and start with Maxwell’s equations, assuming a time-harmonic field and isotropic nonmagnetic medium

where E is the electric field, H is the magnetic field, ω is the angular frequency, and ε is the permittivity. From Faraday’s Law, we have
![]()
which is equivalent to the system of equations
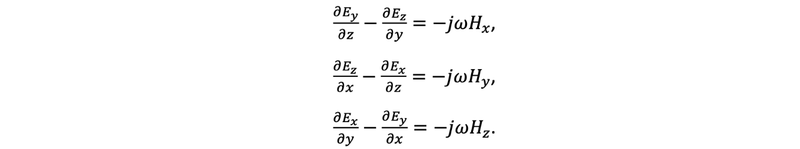
Similarly, from Ampere’s Law, we can obtain three additional equations
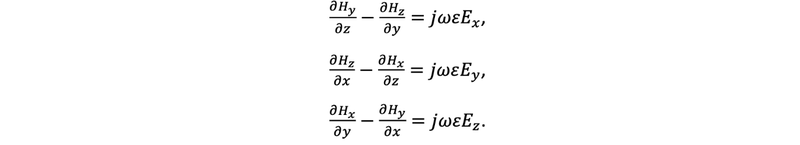
Here, each field component has a spatial dependence, e.g. Ex=Ex(x,y,z). Now without loss of generality we assume our mode solving plane is the xy plane and the guided mode propagates in the z direction. That is, we assume the fields have a z dependence of e-jβz. Combining this assumption with the system of equations above, we arrive at the new system of equations only for the transverse fields Ex(x,y), Ey(x,y), … as
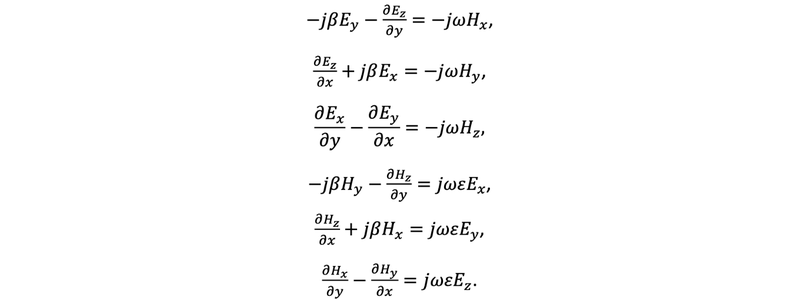
This system of equations can now be numerically solved via different methods such as the finite difference method as implemented in Tidy3D’s mode solver. This calculation takes several steps:
1. Discretization of the Computational Domain
First, the cross-section of the waveguide is divided into a grid where each point on the grid will have an associated electric and magnetic field value. The grid can be uniform or non-uniform. The grid size needs to be sufficiently fine to resolve the mode profile.
2. Finite Difference Approximation of Derivatives
The partial derivatives in the equations are replaced with finite differences. For example, the derivative of Ex with respect to y at point i,j can be approximated as
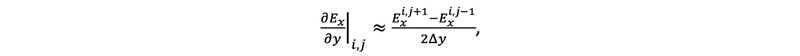
where Δy is the spacing between the grid points in the y direction.
3. Forming the Algebraic System
Once the partial derivatives are replaced with finite differences, the equations turn into algebraic equations. The discretized equations for every point in the domain form a large matrix equation
![]()
where A is a matrix representing the coefficients from the finite difference approximations of the equations. X is the vector of unknowns (field components at each grid point).
4. Solving the Algebraic System
Solving this large system of equations becomes an eigenvalue problem that can be solved numerically. Each eigenvalue corresponds to a different mode’s propagation constant, and each eigenvector gives the corresponding mode’s field distribution.
Applications
1. Waveguide and Optical Fiber Design and Analysis
There are several occasions where we would like to run the mode solver. First of all, the mode solver is essential for waveguide design. Photonic researchers and engineers can use it to calculate mode profiles, effective indices, group indices, and polarization properties. See the following tutorials to learn how to use mode solver as well as the waveguide plugin in Tidy3D:
Tutorial 1: Using the mode solver for optical mode analysis
Tutorial 2: Using the waveguide plugin to analyze waveguide modes
2. Mode Coupling and Conversion Analysis
Furthermore, mode solver is an important tool in coupler and splitter designs. When designing a coupler or splitter, we often need to compute the phase matching condition, which requires accurate calculation of the effective indices of different modes on different waveguides. Based on the mode solving results, one can also derive other quantities of interest such as the overlap integral of two modes, which indicates mode matching and efficiency in mode conversion. We demonstrate mode analysis for coupler design in the following examples:
Example 1: Polarization splitter and rotator based on 90 degree bends
Example 2: 8-Channel mode and polarization de-multiplexer
Example 3: Broadband directional coupler
Example 4: Exceptional coupling for waveguide crosstalk reduction
Example 5: Broadband bi-level taper polarization rotator-splitter
3. Excitation Mode Inspection
In FDTD simulations for photonic components, we often use a mode source to introduce a specific mode into the simulation as excitation, while using mode monitors to track mode transmission and conversion. Before running the FDTD, we can use the mode solver to inspect all the supported modes at the input waveguide and ensure that the desired one is selected as the source, as demonstrated in the following examples:
Example 1: Waveguide Y junction
Example 2: Photonic crystal waveguide polarization filter
Example 3: Plasmonic waveguide sensor for carbon dioxide detection
Notice that both the mode source and mode monitor utilize the same mode-solving algorithm under the hood, and they are used ubiquitously in integrated photonics related examples such as
Example 1: Inverse taper edge coupler
Example 2: Uniform grating coupler
Example 3: Focusing apodized grating coupler
Example 4: Thin film lithium niobate adiabatic waveguide coupler
Example 5: 1x4 MMI power splitter
Example 6: Compact polarization splitter-rotator
Example 7: THz integrated demultiplexer/filter based on a ring resonator








