TIDY3D
LEARNING CENTER

Frequently Asked Questions
About Tidy3D
How is using Tidy3D billed?
The Tidy3D client that is used for designing simulations and analyzing the results is free and open source. We only bill the run time of the solver on our server, taking only the compute time into account (as opposed to overhead, e.g., during uploading). When a task is uploaded to our servers, we will print the maximum incurred cost in FlexCredit. This cost is also displayed in the online interface for that task. This value is determined by the cost associated with simulating the entire time stepping specified. This cost will be pro-rated if early shutoff is detected and the simulation is completed before the time stepping period. For more questions or to purchase FlexCredit, please contact us at support@flexcompute.com.
What is Tidy3D?
Can I get a discount as a student or teacher?
What are the advantages of Tidy3D compared to traditional EM simulators?
Do I have to know Python programming to use Tidy3D?
What is a FlexCredit?
FlexCredit is Flexcompute’s way of measuring computing power. It’s a unit we created to make it easier to understand and buy computing power.
One FlexCredit is equivalent to about 50 hours of CPU core time when using the traditional FDTD method. That’s the equivalent of running a computer processor core for two days straight, just for one FlexCredit! If you have 60 FlexCredits, it’s like having a 4-core CPU (which is a pretty powerful computer) running non-stop, 24 hours a day, for a full month.
This makes it simple for our customers and employees. Instead of trying to communicate in terms of CPU hours or cores, they just need to know how many FlexCredits they need for their project. It’s like buying time on a supercomputer but in a more straightforward, more understandable way.
How many CPU hours is one FlexCredit comparable to?
One FlexCredit is equivalent to about 50 hours of CPU core time when using the traditional FDTD method. That’s the equivalent of running a computer processor core for two days straight, just for one FlexCredit!
If you have 60 FlexCredits, it’s like having a 4-core CPU (which is a pretty powerful computer) running non-stop, 24 hours a day, for an entire month.
Does Tidy3D have a graphical user interface (GUI)?
Tidy3D comes with a feature-rich graphical user interface (GUI) that offers many tools to create and run electromagnetic simulations with ease and intuitiveness. With Tidy3D GUI, you can quickly analyze simulation results, conduct parameter sweeps, perform mode analysis, access simulation information, and manage your account. Additionally, a complete Python notebook development environment is included, allowing you to utilize the flexibility of Tidy3D Python without installing the client interface.
Can I do a free trial to evaluate the capabilities of Tidy3D before purchasing it?
Yes. Suppose you are new to Tidy3D and would like to experience ultrafast electromagnetic simulations. In that case, you can apply for a free trial, which allows you to test many small to medium-sized simulations. The free trial aims to familiarize you with Tidy3D and evaluate its capabilities for your project. During the trial period, we provide full technical support to answer any questions you might have about using Tidy3D.
Installation and Help
How can I install the Python client of Tidy3D?
How do I see the version of Tidy3D I am using?
tidy3d, runprint(tidy3d.__version__)python -c "import tidy3d; print(tidy3d.__version__)"
Can I try Tidy3D before installing the Python client on my computer?
If you want to try Tidy3D, you don’t need to install Python. First, you’ll need to sign up for a free user account. Then you can try both, the feature-rich Tidy3D GUI interface and a pre-installed Tidy3D Python notebook development environment.
Simulations
How do I run a simulation and access the results?
Submitting and monitoring jobs and downloading the results are all done through our web API. After a successful run, all data for all monitors can be downloaded in a single .hdf5 file using tidy3d.web.load(), and the raw data can be loaded into a SimulationData object.
From the SimulationData object, one can grab and plot the data for each monitor with square bracket indexing, inspect the original Simulation object, and view the log from the solver run. For more details, see this beginer tutorial and this advanced tutorial.
How to submit a simulation in Python to the server?
sim_data = tidy3d.web.run(simulation, task_name='my_task', path='out/data.hdf5')job = tidy3d.web.Job(simulation, task_name)run method assim_data = job.run(path)sim_data.How do I upload a job to the web without running it so I can inspect it first?
job object using tidy3d.web.Job, you can upload it to our servers with web.upload(simulation, task_name="task_name", verbose=verbose) and it will not run until you explicitly tell it to do so with web.start(job.task_id). To monitor the simulation's progress and wait for its completion, use web.monitor(job.task_id, verbose=verbose). After running the simulation, you can load the results using sim_data = web.load(job.task_id, path="out/simulation.hdf5", verbose=verbose). In this notebook, you will find detailed information on how to run simulations using the web API.How do I monitor the progress of a simulation?
web.run() method shows the simulation progress by default. When uploading a simulation to the server without running it, you can use the web.monitor(task_id), job.monitor(), or batch.monitor() methods to display the progress of your simulation(s). You can find detailed information on submitting simulation to the server in this tutorial.How do I load the results of a simulation?
After the simulation is complete, you can load the results into a SimulationData object by its task_id using:
sim_data = web.load(task_id, path="outt/sim.hdf5", verbose=verbose)The web.load() method is very convenient to load and postprocess results from simulations created using Tidy3D GUI.
How do I load the results of a job that has already been finished without knowing the task ID?
The job container has a convenient method to save and load the results of a job that has already finished without needing to know the task_id, as below:
# Saves the job metadata to a single file.
job.to_file("data/job.json")
# You can exit the session, break here, or continue in new session.
# Load the job metadata from file.
job_loaded = web.Job.from_file("data/job.json")
# Download the data from the server and load it into a SimulationData object.
sim_data = job_loaded.load(path="data/sim.hdf5")How do I access the original Simulation object that created the data?
To access the original Simulation object that created the simulation data you can use
# Run the simulation.
sim_data = web.run(simulation, task_name='task_name', path='out/sim.hdf5')
# Get a copy of the original simulation object.
sim_copy = sim_data.simulationHow do I save and load the SimulationData object?
sim_data.to_file(fname='path/to/file.hdf5') to save a SimulationData object to a HDF5 file, and sim_data = SimulationData.from_file(fname='path/to/file.hdf5') to load a SimulationData object from a HDF5 file.How do I save and load any Tidy3D object?
obj is an instance of ObjClass, save and load it with obj.to_file(fname='path/to/file.json') and obj = ObjClass.from_file(fname='path/to/file.json'), respectively.How do I get all data in a Tidy3d object as a dictionary?
To get all the data in a Tidy3D object obj as a dictionary, you should use the command obj.dict().
How do I estimate how many credits my simulation will take?
We can get the cost estimate of running the task before running it. This prevents us from accidentally running large jobs we set up by mistake. The estimated cost is the maximum cost corresponding to running all the time steps. To do so, run a code like below:
# initializes job, puts task on server (but doesnt run it)
job = web.Job(simulation=sim, task_name="job", verbose=verbose)
# estimate the maximum cost
estimated_cost = web.estimate_cost(job.task_id)
print(f'The estimated maximum cost is {estimated_cost:.3f} Flex Credits.')See this notebook to obtain other details about submitting simulations to the server.
How do I see the cost of my simulation?
To obtain the cost of a simulation, you can use the function tidy3d.web.real_cost(task_id). In the example below, a job is created, and its cost is estimated. After running the simulation, the real cost can be obtained. It is important to note that the real cost may not be available immediately after the simulation is finished.
import time
# initializes job, puts task on server (but doesnt run it)
job = web.Job(simulation=sim, task_name="job", verbose=verbose)
# estimate the maximum cost
estimated_cost = web.estimate_cost(job.task_id)
print(f'The estimated maximum cost is {estimated_cost:.3f} Flex Credits.')
# Runs the simulation.
sim_data = job.run(path="data/sim_data.hdf5")
time.sleep(5)
# Get the billed FlexCredit cost after a simulation run.
cost = web.real_cost(job.task_id)How can I reduce the simulation cost?
The cost of a simulation is primarily affected by the number of grid points and time steps. To reduce the simulation cost, you can take specific actions. However, it’s essential to gather relevant information about the simulation first to help you in this process.
# Initializes job, puts task on server (but doesn't run it).
job = tidy3d.web.Job(simulation=sim, task_name="job", verbose=verbose)
# Estimate the maximum cost before running the simulation.
estimated_cost = tidy3d.web.estimate_cost(job.task_id)
print(f'The estimated maximum cost is {estimated_cost:.3f} Flex Credits.')
# Run the simulation.
sim_data = tidy3d.web.run(simulation=sim, task_name="task", path="data/data.hdf5", verbose=True)
# Print simulation information such as grid points and time steps.
print(sim_data.log)Symmetry
In Tidy3D simulations, field symmetries can significantly reduce computational time and FlexCredit cost, sometimes by factors of 1/2, 1/4, or even 1/8. Therefore, symmetry is preferred whenever applicable. However, it is crucial to set up the symmetry correctly to avoid inaccurate results. For a more detailed explanation of symmetry, please refer to the dedicated tutorial.
Meshing Strategy
To reduce the number of grid points (and time steps) in a simulation, you can adjust the GridSpec specifications. You have the option to choose between AutoGrid, UniformGrid, or CustomGrid for each simulation direction. Starting with the default object AutoGrid is generally a good strategy to discretize the entire simulation domain. You can then fine-tune the mesh by increasing grid resolution for directions or regions with smaller geometric features or high field gradients. You can also relax the discretization along directions of invariant geometry, such as the propagation direction of channel waveguides. Another way to enhance simulation accuracy while keeping the grid points small is by defining an override structure.
Shutoff
By default, Tidy3D periodically checks the total field intensity left in the simulation and compares that to the maximum total field intensity recorded at previous times. If it is found that the ratio of these two values is smaller than \(10^{-5}\), the simulation is terminated as the fields remaining in the simulation are deemed negligible. The shutoff value can be controlled using the tidy3d.Simulation.shutoff parameter, or completely turned off by setting it to zero. In most cases, the default behavior ensures that results are correct while avoiding unnecessarily long run times. The Flex Unit cost of the simulation is also proportionally scaled down when early termination is encountered.
Boundary Conditions
When running simulations, it’s important to use appropriate boundary conditions to absorb incoming waves and minimize reflection accurately. The tidy3d.PML boundary condition is generally the best choice, as it can absorb waves from all angles with minimal reflection. However, in some instances where an angled structure or dispersive materials are present within the PML, you may need to use the tidy3d.Absorber instead. While the absorber performs a similar function to the PML, it has a slightly higher reflection rate and requires more computation, resulting in higher simulation costs.
See this notebook for more details on setting up boundary conditions.
How do I print the task log file?
To keep track of the details of a simulation, a log file is created that contains information about the simulation size, symmetries, number of computational grid points, time steps, shut-off condition, and the time taken for simulation setup and running. If you need to print out the log file of a simulation, you can use the command print(sim_data.log).
What are the units used in the simulation?
We generally assume the following physical units in component definitions:
- Length: micron (μm, $10^{-6}$ meters)
- Time: Second ($s$)
- Frequency: Hertz ($Hz$)
- Electric conductivity: Siemens per micron ($S/μm$)
Thus, the user should be careful, for example, to use the speed of light in μm/s when converting between wavelength and frequency. The built-in speed of light C_0 has a unit of μm/s.
For example:
wavelength_um = 1.55
freq_Hz = td.C_0 / wavelength_um
wavelength_um = td.C_0 / freq_HzCurrently, only linear evolution is supported, and so the output fields have an arbitrary normalization proportional to the amplitude of the current sources, which is also in arbitrary units. In the API Reference, the units are explicitly stated where applicable.
Output quantities are also returned in physical units, with the same base units as above. For time-domain outputs as well as frequency-domain outputs when the source spectrum is normalized out (default), the following units are used:
- Electric field: Volt per micron ($V/μm$)
- Magnetic field: Ampere per micron ($A/μm$)
- Flux: Watt ($W$)
- Poynting vector: Watt per micron squared ($W/μm^{2}$)
- Modal amplitude: Square root of watt ($W^{1/2}$)
If the source normalization is not applied, the electric field, magnetic field, and modal amplitudes are divided by Hz, while the flux and Poynting vector are divided by $Hz^{2}$.
How to run a 2D simulation in Tidy3D?
tidy3d.Simulation(size=[size_x, size_y, 0])). Additionally, specify a tidy3D.Periodic boundary condition in that direction. For an example of running a 2D simulation in Tidy3D, see the 2D ring resonator notebook.Why the simulation time for the exact same simulation can vary?
Depending on the size of the simulation task submitted, our cloud always tries to dynamically allocate the optimal amount of computational resources to run this task. When the server is busy, the resources could become limited, so a smaller amount of resources are assigned to run the task, making the simulation time slightly longer than usual. However, this should be relatively rare as we constantly monitor the status of our server and ensure ample hardware resources are available at all times.
How long should I run the simulation?
The frequency-domain response obtained in the FDTD simulation only accurately represents the continuous-wave response of the system if the fields at the beginning and at the end of the time stepping are (very close to) zero. So, you should run the simulation for enough time to allow the electromagnetic fields to decay to negligible values within the simulation domain.
When dealing with light propagation in a NON-RESONANT device, like a simple optical waveguide, a good initial guess to simulation run_time would be a few times the largest domain dimension ($L$) multiplied by the waveguide mode group index ($n_g$), divided by the speed of light in a vacuum ($c_0$), plus the source_time.
tidy3d.Simulation.shutoff parameter, or completely turned off by setting it to zero. In most cases, the default behavior ensures that results are correct while avoiding unnecessarily long run times. The Flex Unit cost of the simulation is also proportionally scaled down when early termination is encountered.Can you convert a lumerical script file to Tidy3D?
This repo offers a limited ability to convert .lsf project files to Tidy3D skeleton files in Python. Not every command in the lsf file is covered. The lsf project files often have default values/conventions that are not specified, so the created Tidy3D script will often need additional specification. Always be sure to check over the created Tidy3D script to see if any values are missing or if any objects have not been parsed.
Parameter Sweep
How do I run a parameter sweep?
tidy3d.web.Batch.run() to upload, run, and get the simulations results in a tidy3d.web.BatchData object. For example:# Create a dictionary including all the simulations.
sims = {"sim_1": sim_1, "sim_2": sim_2, "sim_3": sim_3}
# Build a Batch object.
batch = tidy3d.web.Batch(simulations=sims, verbose=True)
# Run all the simulations and get the results.
batch_results = batch.run(path_dir="data")# Create a dictionary including all the simulations.
sims = {"sim_1": sim_1, "sim_2": sim_2, "sim_3": sim_3}
# Run all the simulations and get the results.
batch_results = batch.run_async(sims, path_dir="data")After running the simulations, you can get the results from the tidy3d.web.BatchData object directly, using for example sim_data_1 = batch_results["sim_1"]. Or iterating over it in a loop, as below:
sim_data = []
for task_name, sim_data in batch_results.items():
sim_data.append(sim_data)In this notebook you will find a detailed example of how to run parameter sweeps.v
How do I submit multiple simulations?
tidy3d.web.Batch.run() to upload, run, and get the simulations results in a tidy3d.web.BatchData object. For example:# Create a dictionary including all the simulations.
sims = {"sim_1": sim_1, "sim_2": sim_2, "sim_3": sim_3}
# Build a Batch object.
batch = tidy3d.web.Batch(simulations=sims, verbose=True)
# Run all the simulations and get the results.
batch_results = batch.run(path_dir="data")# Create a dictionary including all the simulations.
sims = {"sim_1": sim_1, "sim_2": sim_2, "sim_3": sim_3}
# Run all the simulations and get the results.
batch_results = batch.run_async(sims, path_dir="data")After running the simulations, you can get the results from the tidy3d.web.BatchData object directly, using for example sim_data_1 = batch_results["sim_1"]. Or iterating over it in a loop, as below:
sim_data = []
for task_name, sim_data in batch_results.items():
sim_data.append(sim_data)In this notebook, you will find a detailed example of how to run parameter sweeps.
How to load a batch result?
When a batch is created, a batch.hdf5 file will be created automatically. Users can use this file to collect all the simulation results from the batch. First, load the batch.hdf5 file by
batch = web.Batch.from_file(“folder_name/batch.hdf5”)Then download and load all simulations results into a BatchData object by
batch_results = batch.load(path_dir=“data”)Then, you can further extract the result for each simulation from batch_results.
How do I loop through tidy3d.web.BatchData without loading all of the data into memory?
sim_data_1 = batch_results["sim_1"]. Or iterating over it in a loop, as below:sim_data = []
for task_name, sim_data in batch_results.items():
sim_data.append(sim_data)So, you will get access to the tidy3d.SimulationData instances to perform your postprocessing.
How do I save or load a tidy3d.web.Batch so I can work with it later?
to_file(path) and from_file(path) methods that will export and load their metadata as JSON files. This is especially useful for loading batches for long analysis after they have run. For example, one can save the batch information to file and load the batch later if one needs to disconnect from the service while the jobs are running.# Save batch metadata.
batch.to_file("data/batch_data.json")
# Load batch metadata into a new batch.
loaded_batch = web.Batch.from_file("data/batch_data.json")
Simulation Troubleshoot
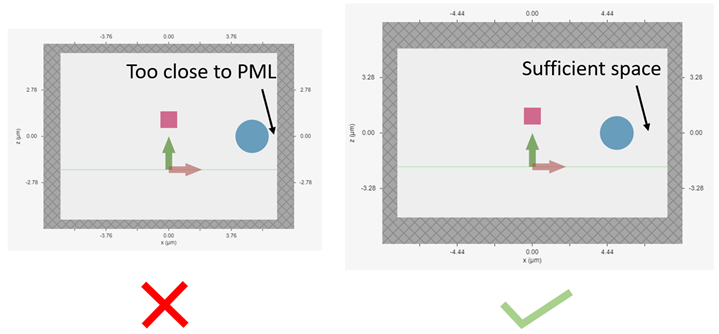
Why is a simulation diverging?
Sometimes, a simulation is numerically unstable and can result in divergence. All known cases where this may happen are related to PML boundaries and/or dispersive media. Below is a checklist of things to consider.
- For dispersive materials with $\epsilon_{\infty} < 1$, decrease the value of the Courant stability factor to below $\sqrt{\epsilon_{\infty}}$.
- Move PML boundaries further away from structure interfaces inside the simulation domain, or from sources that may be injecting evanescent waves, like PointDipole, UniformCurrentSource, or CustomFieldSource.
- Make sure structures are translationally invariant into the PML, or if not possible, use Absorber boundaries.
- Remove dispersive materials extending into the PML, or if not possible, use Absorber boundaries.
- If using our fitter to fit your own material data, ensure you are using the
plugins.StableDispersionFitter. - If none of the above work, try using StablePML or Absorber boundaries anyway (note: these may introduce more reflections than in usual simulations with regular PML).
How can I troubleshoot a diverged FDTD simulation?
Structures Inserted into PML at an Angle
Dispersive Material into PML
Evanescent Field Leaks into PML
Gain Medium from Fitting
Courant Factor is Too Large
Additional Notes on Absorber
Contact Tidy3D Support
Why did my simulation finish early?
By default, Tidy3D periodically checks the total field intensity left in the simulation, and compares that to the maximum total field intensity recorded at previous times. If it is found that the ratio of these two values is smaller than \(10^{-5}\), the simulation is terminated as the fields remaining in the simulation are deemed negligible. The shutoff value can be controlled using the Simulation.shutoff parameter or completely turned off by setting it to zero. In most cases, the default behavior ensures that results are correct while avoiding unnecessarily long run times. The Flex Unit cost of the simulation is also proportionally scaled down when early termination is encountered.
Should I make sure that fields have fully decayed by the end of the simulation?
When early termination happens, you may sometimes get a warning that the fields remaining in the simulation at the end of the run have not decayed down to the pre-defined shutoff value. This should usually be avoided (that is to say, Simulation.run_time should be increased), but there are some cases in which it may be inevitable. The important thing to understand is that in such simulations, frequency-domain results cannot always be trusted. The frequency-domain response obtained in the FDTD simulation only accurately represents the continuous-wave response of the system if the fields at the beginning and at the end of the time stepping are (very
close to) zero. That said, there could be non-negligible fields in the simulation. Yet, the data recorded in a given monitor can still be accurate if the leftover fields are no longer passing through the monitor volume. From the point of view of that monitor, fields have already fully decayed. However, there is no way to automatically check this. The accuracy of frequency-domain monitors when fields have not fully decayed is also discussed in one of our FDTD 101
videos.
The primary use case in which you may want to ignore this warning is when you have high-Q modes in your simulation that would require an extremely long run time to decay. In that case, you can use the ResonanceFinder plugin to analyze the modes, as well as field monitors with apodization to capture the modal profiles. The only thing to note is that the normalization of these modal profiles would be arbitrary and would depend on the exact run time and apodization definition. An example of such a use case is presented in our high-Q photonic crystal cavity case study.
Can I have structures larger than the simulation domain?
Structures can indeed be larger than the simulation domain in Tidy3D. In such cases, Tidy3D will automatically truncate the geometry that goes beyond the domain boundaries. For best results, structures that intersect with absorbing boundaries or simulation edges should extend all the way through. In many such cases, an “infinite” size td.inf can be used to define the size along that dimension.
Why can I not change Tidy3D instances after they are created?
You may notice in Tidy3D versions 1.5 and above that it is no longer possible to modify instances of Tidy3D components after they are created. Making Tidy3D components immutable like this was an intentional design decision intended to make Tidy3D safer and more performant.
For example, Tidy3D contains several "validators" on input data. If models are mutated, we can't always guarantee that the resulting instance will still satisfy our validations, and the simulation may be invalid.
Furthermore, making the objects immutable allows us to cache the results of many expensive operations. For example, we can now compute and store the simulation grid without worrying about the value becoming stale later, which significantly speeds up plotting and other operations.
If you have a Tidy3D component that you want to recreate with a new set of parameters, instead of obj.param1 = param1_new, you can call obj_new = obj.copy(update=dict(param1=param1_new)). Note that you may also pass more key value pairs to the dictionary in update. Also, note you can use a convenience method obj_new = obj.updated_copy(param1=param1_new), which is just a shortcut to the obj.copy() call above.
Why does the kernel crash sometimes when using the web-based Python notebook?
The web-based Python notebook environment in tidy3d.simulation.cloud only has access to 4 GB of memory. When running a large simulation or complex optimizations, the memory needed to process the data could exceed the limit, causing the kernel to crash. In this case, we recommend installing Tidy3D on your local computer by following the installation guide and video. It will then use your computer memory, which is typically larger than 4 GB.
Mediums
How do I include material dispersion?
Dispersive materials are supported in Tidy3D, and we provide an extensive material library with pre-defined materials. Standard dispersive material models can also be defined. If you need help inputting a custom material, let us know!
It is important to keep in mind that dispersive materials are inevitably slower to simulate than their dispersion-less counterparts, with complexity increasing with the number of poles included in the dispersion model. For simulations with a narrow range of frequencies of interest, it may sometimes be faster to define the material through its real and imaginary refractive index at the center frequency. This can be done by defining directly a value for the real part of the relative permittivity $\mathrm{Re}(\epsilon_r)$ and electric conductivity $\sigma$ of a Medium, or through a real part $n$ and imaginary part $k$. The relationship between the two equivalent models is $\mathrm{Re}(\epsilon_r) = n^2 - k^2$, $\mathrm{Im}(\epsilon_r) = 2nk$, and $\sigma = 2 \pi f \epsilon_0 \mathrm{Im}(\epsilon_r)$.
In the case of (almost) lossless dielectrics, the dispersion could be negligible in a broad frequency window, but generally, it is importat to keep in mind that such a material definition is best suited for single-frequency results.
For lossless, weakly dispersive materials, the best way to incorporate the dispersion without doing complicated fits and without slowing the simulation down significantly is to provide the value of the refractive index dispersion $\mathrm{d}n/\mathrm{d}\lambda$ in Sellmeier.from_dispersion(). The value is assumed to be at the central frequency or wavelength (whichever is provided), and a one-pole model for the material is generated. These values are, for example, readily available from the refractive index database.
Can I import my own tabulated material data?
Yes, users can import their own tabulated material data and fit it using one of Tidy3D’s dispersion fitting tools. The FastDispersionFitter tool performs an optimization to find a medium defined as a dispersive PoleResidue model that minimizes the RMS error between the model results and the data. The user can provide data through one of the following methods:
- Numpy arrays directly by specifying
wvl_um,n_data, and optionallyk_data. - A data file with the
from_fileutility function. The data file has columns for wavelength ($μm$), the real part of the refractive index ($n$), and the imaginary part of the refractive index ($k$). $k$ data is optional. Note:from_fileusesnp.loadtxtunder the hood, so additional keyword arguments for parsing the file follow the same format asnp.loadtxt. - URL link to a CSV/TXT file that contains wavelength ($μm$), $n$, and optionally $k$ data with the
from_urlutility function. URL can come from refractiveindex.
This notebook provides detailed instructions and examples of using the fitter.
How do I create a lossy material (with a conductivity)?
To create a lossy material including conductivity, use the tidy3d.Medium object and set the conductivity parameter. For example:
lossy_medium = tidy3d.Medium(permittivity=2.0, conductivity=1.0)How do I create a material from n, k values at a given frequency?
To create a material from the real ($n$) and imaginary ($k$) parts of refractive index, use the tidy3d.Medium.from_nk(). For example:
nk_medium = tidy3d.Medium.from_nk(n=2.0, k=1.0, freq=freq0)Negative $k$ value corresponds to a gain medium. It is only allowed when the parameter
allow_gainis set toTrue.
How do I create a material from optical n, k data?
You can import your own tabulated material data and fit it using one of Tidy3D’s dispersion fitting tools. The FastDispersionFitter tool performs an optimization to find a medium defined as a dispersive PoleResidue model that minimizes the RMS error between the model results and the data. The user can provide data through one of the following methods:
- Numpy arrays directly by specifying
wvl_um,n_data, and optionallyk_data. - A data file with the
from_fileutility function. The data file has columns for wavelength ($μm$), the real part of the refractive index ($n$), and the imaginary part of the refractive index ($k$). $k$ data is optional. Note:from_fileusesnp.loadtxtunder the hood, so additional keyword arguments for parsing the file follow the same format asnp.loadtxt. - URL link to a CSV/TXT file that contains wavelength ($μm$), $n$, and optionally $k$ data with the
from_urlutility function. URL can come from refractiveindex.
This notebook provides detailed instructions and examples on using the fitter.
How do I create a dispersive material from model parameters?
To create a dispersive material from model parameters, you only need to instantiate the medium object and provide its parameters. For example, debye_medium = td.Debye(eps_inf=2.0, coeffs=[(1,2),(3,4)]).
How do I create an anisotropic material?
To create fully anisotropic mediums including all 9 components of the permittivity and conductivity tensors, you can use the tidy3d.FullyAnisotropicMedium object. The provided permittivity tensor and the symmetric part of the conductivity tensor must have coinciding main directions. However, a non-symmetric conductivity tensor can be used to model magneto-optic effects. Note that dispersive properties and subpixel averaging are currently not supported for fully anisotropic materials.
perm = [[2, 0, 0], [0, 1, 0], [0, 0, 3]]
cond = [[0.1, 0, 0], [0, 0, 0], [0, 0, 0]]
anisotropic_dielectric = FullyAnisotropicMedium(permittivity=perm, conductivity=cond)Alternatively, you can create a diagonally anisotropic material, using the tidy3d.AnisotropicMedium(xx=medium_xx, yy=medium_yy, zz=medium_zz) object, and then include three medium objects defining the diagonal elements of the permittivity tensor. In this case, the medium objects can be of type Medium, PoleResidue, Sellmeier, Lorentz, Debye, or Drude. For example:
medium_xx = Medium(permittivity=4.0)
medium_yy = Medium(permittivity=4.1)
medium_zz = Medium(permittivity=3.9)
anisotropic_dielectric = AnisotropicMedium(xx=medium_xx, yy=medium_yy, zz=medium_zz)How do I create an active material?
allow_gain=True in any medium, e.g. tidy3d.Medium(permittivity=2.0, conductivity=-1.0, allow_gain=True).How do I create a spatially varying material?
How do I export a spatially varying medium dataset to HDF5?
To export a spatially varying medium dataset to a HDF5 file you should use the to_hdf5(filename) method. In the example below, we illustrate how to do that after creating a tidy3d.CustomMedium.
# The coordinate for the refractive index data that includes x, y, z, and frequency
X = np.linspace(-20, 20, 100) # x grid
Y = np.linspace(-20, 20, 100) # y grid
Z = [0] # z grid
# Create a permittivity dataset and a custom medium.
n_data = np.ones((100, 100, 1, 1)) * 12
n_dataset = tidy3d.SpatialDataArray(n_data, coords=dict(x=X, y=Y, z=Z, f=[freq0]))
data = tidy3d.PermittivityDataset(eps_xx=n_dataset, eps_yy=n_dataset, eps_zz=n_dataset)
mat_custom = tidy3d.CustomMedium(eps_dataset=data, interp_method="nearest")
# Export the custom medium dataset to HDF5.
mat_custom.to_hdf5(fname="CustomMedium.hdf5")How do I load a commonly used dispersive material?
from tidy3d import material_library
silver = material_library['Ag']['Rakic1998BB']The key of the dictionary is the abbreviated material name. Some materials have multiple variant models, in which case the second key is the “variant” name.
How can I define a 2D material?
You can create a 2D material using the tidy3d.Medium2D object. This is especially helpful for building very thin materials, like metal layers.
t_copper = 0.0001 # Thickness of the copper layer.
sigma_copper = 50 # Copper conductivity in S/um.
# Define copper as a Medium2D.
copper = td.Medium2D.from_medium(
td.Medium(conductivity=sigma_copper), thickness=t_copper
)How can I define graphene?
You can create a graphene medium using tidy3d.Graphene, which defines a parametric surface conductivity model for graphene. For example:
gamma = 0.0033 # Scattering rate (eV).
mu_c = 0.5 # Graphene chemical potential (eV).
temp = 300 # Temperature (K).
scaling = 2 # Number of graphene layers.
graphene = td.material_library["graphene"](
gamma=gamma, mu_c=mu_c, temp=temp, scaling=scaling
).medium
# or
# graphene = tidy3d.Graphene(
# gamma=gamma, mu_c=mu_c, temp=temp, scaling=scaling
# ).mediumHow can I define a nonlinear material?
To create nonlinear material, you should specify a tidy3d.NonlinearSusceptibility to the nonlinear_spec parameter of any medium. For example:
medium = tidy3d.Medium(permittivity=2, nonlinear_spec=tidy3d.NonlinearSusceptibility(chi3=1, numiters=5))chi3 is the nonlinear susceptibility, and numiters is the number of iterations for solving nonlinear constitutive relation.Structures
How do I import a structure from a GDSII file?
In Tidy3D, complex structures can be imported from GDSII files via the third-party gdstk package, which you can install running pip install gdstk. To load the geometry from a GDSII file, you should select the cell with the geometry you want. It is usually easier to verify that we can find the correct one by name first, for example:
# Load a GDSII library from the file.
lib_loaded = gdstk.read_gds(gds_path)
# Create a cell dictionary with all the cells in the file.
all_cells = {c.name: c for c in lib_loaded.cells}
print("Cell names: " + ", ".join(all_cells.keys()))Then you can construct Tidy3D geometries from the GDS cell just loaded, along with other information such as the axis, sidewall angle, and bounds of the "slab" using tidy3d.Geometry.from_gds(). When loading GDS cell as the cross section of the device, we can tune reference_plane to set the cross-section to lie at bottom, middle, or top of the generated geometry with respect to the axis. E.g. if axis=1, bottom refers to the negative side of the y-axis, and top refers to the positive side of the y-axis. Additionally, we can optionally dilate or erode the cross section by setting dilation. A negative dilation corresponds to erosion. Note, we have to keep track of the gds_layer and gds_dtype used to define the GDS cell earlier, so we can load the right components.
wg_height = 0.22
dilation = 0.02
geo = tidy3d.Geometry.from_gds(
gds_cell=all_cells["TOP"],
gds_layer=0,
gds_dtype=0,
axis=2,
slab_bounds=(-0.11, 0.11),
reference_plane="bottom",
)You can find more details on importing GDSII files in these notebooks: Importing GDS files; Defining self-intersecting polygons.
How can I import a structure from STL files?
To use the STL import functionality, you must install Tidy3D as pip install "tidy3d[trimesh]", which will install optional dependencies for processing surface meshes. Then you can use the tidy3d.TriangleMesh.from_stl() function. In the following example, we will import a simple box geometry from a STL file.
# Make the geometry object representing the STL solid from the STL file stored on disk
box = tidy3d.TriangleMesh.from_stl(
filename="./misc/box.stl",
scale=1, # The units are already microns as desired, but this parameter can be used to change units [default: 1].
origin=(
0,
0,
0,
), # This can be used to set a custom origin for the stl solid [default: (0, 0, 0)]
solid_index=None, # Sometimes, there may be more than one solid in the file; use this to select a specific one by index.
)See this example for a complete reference on importing STL files.
How do I export a structure to GDSII format?
In Tidy3D, you can export structures to GDSII file via the third-party gdstk package, which you can install running pip install gdstk. The example below creates a simple geometry and then exports it to GDSII:
# Create a gds cell to add the structures to.
geo_cell = gdstk.Cell("TOP")
# Make a box and add it to the cell.
box = gdstk.rectangle((-1, 1), (-1, 1), layer=0)
geo_cell.add(box)
# Create a library for the cell and save it.
gds_path = "box.gds"
lib = gdstk.Library()
lib.add(box_cell)
lib.write_gds(gds_path)The method .to_gds_file() is another option to export a geometry to GDSII. For example:
# Create a simulation object.
sim = td.Simulation(
size=sim_size,
grid_spec=td.GridSpec.uniform(dl=dl),
structures=structures,
boundary_spec=td.BoundarySpec.all_sides(boundary=td.PML()),
)
# Export the structure to GDSII.
sim.to_gds_file(fname="sim.gds",
z=0,
permittivity_threshold=5,
frequency=f0,
)You can find more details on exporting structures to GDSII files in the notebook Importing GDS files.
How do I create a box?
You can create a box geometry using the tidy3d.Box object. You can specify the center and size parameters, as below:
box = tidy3d.Box(center=(1,2,3), size=(2,2,2))Or you can use the tidy3d.Box.from_bounds() method, where you should define the rmin and rmax coordinates of the lower and upper box corners. For example:
box = tidy3d.Box.from_bounds(
rmin=(-10, -1, -0.1),
rmax=(10, 1, 0.1),
)How do I create a sphere?
You can create a sphere using the tidy3d.Sphere object and specifying the center and radius parameters, as below:
box = tidy3d.Box.from_bounds(
rmin=(-10, -1, -0.1),
rmax=(10, 1, 0.1),
)How do I create a cylinder?
You can create a cylinder using the tidy3d.Cylinder object. In the example below we create a cylinder 2 $\mu$m in length, oriented along the z-axis, with a 0.5 $\mu$m radius, and positioned at (-1,1,0). To obtain a conical shape, set the parameters sidewall_angle and reference_plane.
cyl = tidy3d.Cylinder(center=(-1,1,0), radius=0.5, length=2, axis=2)How do I create a polygon?
Use the tidy3d.PolySlab object to create an extruded polygon with an optional sidewall angle along the axis direction. The polygon geometry is defined by the vertices parameter, which receives a list of (d1, d2) coordinates defining the geometry of the polygon face at the reference_plane. The slab_bounds parametere defines the minimum and maximum positions of the slab along the axis dimension. Set the sidewall_angle with respect to the reference_plane to create slanted sidewalls. In addition, you can dilate or erode the polygon by setting positive or negative values to dilation parameter.
vertices = np.array([(0,0), (1,0), (1,1)])
triangle = tidy3d.PolySlab(vertices=vertices, axis=2, slab_bounds=(-1, 1))How do I create a geometry group?
A geometry group is a convenient way to gather multiple geometry objects into one collection. It can significantly improve performance when all the geometries in the group are assigned to the same medium. To create a geometry group, use the tidy3d.GeometryGroup object and set the geometries parameter as below:
cylinders = []
for i in range(0, 4):
c = tidy3d.Cylinder(
axis=2, radius=0.3, center=(i, 0, 0), length=2,
)
cylinders.append(c)
structure = tidy3d.Structure(
geometry=tidy3d.GeometryGroup(geometries=cylinders),
medium=tidy3d.Medium(permittivity=4),
)How do I combine multiple geometries?
You can combine multiple geometries using the tidy3d.ClipOperation object to perform ‘union’, ‘intersection’, ‘difference’, and ‘symmetric_difference’ operations. For example:
box = tidy3d.Box(center=(0,0,0), size=(1, 1, 2))
cyl = tidy3d.Cylinder(center=(1,0,0), radius=0.5, length=2, axis=2)
union = tidy3d.ClipOperation(
operation='union', geometry_a=box, geometry_b=cyl
)
intersection = tidy3d.ClipOperation(
operation='intersection', geometry_a=box, geometry_b=cyl
)
difference = tidy3d.ClipOperation(
operation='difference', geometry_a=box, geometry_b=cyl
)
symmetric_difference = tidy3d.ClipOperation(
operation='symmetric_difference', geometry_a=box, geometry_b=cyl
)When two structures overlap, what is the priority determined?
When two structures overlap, the last ones in the structures list will override the permittivities of the previous structures. This notebook illustrates how to use this rule to create a photonic crystal slab. The holes geometry with a refractive index of 1 overrides the slab permittivities in regions where they overlap, creating the air holes.
# Simulation
sim = td.Simulation(
size=sim_size,
grid_spec=grid_spec,
structures=[slab, holes],
sources=[source],
monitors=[time_series_mnt, field_mnt, far_field_mnt],
run_time=run_time,
boundary_spec=td.BoundarySpec.all_sides(boundary=td.PML()),
symmetry=(1, -1, 1),
shutoff=0,
)How to rotate a geometry?
In Tidy3D, all geometries can be translated, rotated, and scaled. These methods create a new copy of the original geometry with a transformation applied. For example, you can start with a tidy3d.Box centered at the origin and create a copy of it rotated around the z-axis:
box = tidy3d.Box(size=(2, 1, 1))
rotated_box = box.rotated(np.pi / 6, axis=2)
_ = rotated_box.plot(z = 0)See this example for more information.
How to translate a geometry?
In Tidy3D, all geometries can be translated, rotated, and scaled. These methods create a new copy of the original geometry with a transformation applied. For example, you can start with a tidy3d.Box centered at the origin and create a copy of it translated in the x-direction by 2 $\mu m$:
box = tidy3d.Box(size=(2, 1, 1))
box_translated = box.translated(x=2, y=0, z=0)
_ = box_translated.plot(z = 0)See this example for more information.
How to scale a geometry?
In Tidy3D, all geometries can be translated, rotated, and scaled. These methods create a new copy of the original geometry with a transformation applied. For example, you can start with a tidy3d.Box centered at the origin and create a copy of it scaled by a factor of 2 in all directions:
box = tidy3d.Box(size=(2, 1, 1))
box_scaled = box.scaled(x=2.0, y=2.0, z=2.0)
_ = box_scaled.plot(z = 0)See this example for more information.
How can I apply transformations to a geometry?
In Tidy3D, all geometries can be translated, rotated, and scaled. These methods create a new copy of the original geometry with a transformation applied. For example, you can start with a tidy3d.Box centered at the origin and create a copy of it rotated around the z-axis:
box = tidy3d.Box(size=(2, 1, 1))
rotated_box = box.rotated(np.pi / 6, axis=2)
_ = rotated_box.plot(z = 0)Transformed geometries can be further transformed. Composing transformations is as simple as cascading the method calls. In the following example, we create an ellipsoidal prism by scaling a primitive tidy3d.Cylinder and rotating it.
ellipsoid = tidy3d.Cylinder(radius=0.5, length=0.5, axis=1).scaled(x=2, y=1, z=1).rotated(np.pi / 4, axis=1)
_ = ellipsoid.plot(y=0)A tidy3d.Transformed object contains an inner geometry and a transformation, written as a 4 x 4 matrix and applied to the (homogeneous) coordinates of the inner geometry. It is possible to define a Transformed object directly from the inner geometry and the transformation. To help create the most usual transformation matrices, the Transformed class has 3 static methods for translation, rotation, and scaling that can be used and combined (the @ operator can be used for matrix multiplication with numpy arrays).
rot = tidy3d.Transformed.rotation(np.pi / 3, axis=(1, 1, 1))
trans = tidy3d.Transformed.translation(1, 2, 0)
scale = tidy3d.Transformed.scaling(1, 1.25, 1)
# The box is first rotated, then translated, and finally scaled
transformed = td.Transformed(geometry=td.Box(size=(1, 1, 1)), transform=scale @ trans @ rot)See this example for more information.
How do I use clip operations?
You can use the tidy3d.ClipOperation object to combine multiple geometries through ‘union’, ‘intersection’, ‘difference’, and ‘symmetric_difference’ operations. Simply define the geometry_a and the geometry_b and assign them to the clip object. For example:
box = tidy3d.Box(center=(0,0,0), size=(1, 1, 2))
cyl = tidy3d.Cylinder(center=(1,0,0), radius=0.5, length=2, axis=2)
union = tidy3d.ClipOperation(
operation='union', geometry_a=box, geometry_b=cyl
)
intersection = tidy3d.ClipOperation(
operation='intersection', geometry_a=box, geometry_b=cyl
)
difference = tidy3d.ClipOperation(
operation='difference', geometry_a=box, geometry_b=cyl
)
symmetric_difference = tidy3d.ClipOperation(
operation='symmetric_difference', geometry_a=box, geometry_b=cyl
)Which features can I use to create geometries in Tidy3D?
Tidy3D offers four primitive geometric shapes: Box, Cylinder, Sphere, and PolySlab. An extensive array of intricate geometrical configurations can be defined from these fundamental building blocks by manipulating their properties and hierarchical arrangements. For instance, our tutorials on the Luneburg lens waveguide size converter and the Fresnel lens showcase the creation of curved surfaces through the strategic layering of cylindrical elements.
Beyond the in-built primitives, Tidy3D accommodates external geometrical specifications in either the GDS or STL file formats, allowing users to import custom geometries created in their preferred design tools. Additionally, compatibility with external libraries like gdstk and shapely opens the gateway to even more complex geometric possibilities. Using gdstk to create various waveguide structures has been demonstrated in various examples, such as thepolarization splitter and rotator based on 90-degree bends](https://www.flexcompute.com/tidy3d/examples/notebooks/90BendPolarizationSplitterRotator/?__hstc=197414576.85a08fc595b47d0b94ebfa20ba44cd6d.1696006513341.1701896316776.1701901226721.28&__hssc=197414576.3.1701901226721&__hsfp=3209960735). Additionally, you can create complex geometries using the Trimesh library, as demonstrated in this tutorial.
How do I define complex geometries using trimesh?
To define complex geometries using the Trimesh library, you must install Tidy3D as pip install "tidy3d[trimesh]", which will install optional dependencies needed for processing surface meshes. The Trimesh library provides some built-in geometries such as ring (annulus), box, capsule, cone, cylinder, and so on. Let’s create a ring as an example.
n_sections = 100 # How many sections to discretize the mesh.
# Create a ring mesh.
ring_mesh = trimesh.creation.annulus(r_min=9, r_max=10, height=1, sections=n_sections)
# Plot the mesh.
ring_mesh.show()To use this geometry in a Tidy3D simulation, you need to convert the mesh into a tidy3d.TriangleMesh geometry. Use the from_trimesh() method to conviently convert the mesh to a Tidy3D geometry. From there, you can further define the Tidy3D structure and put it into a simulation.
# Define a tidy3d geometry from a mesh.
ring_geo = td.TriangleMesh.from_trimesh(ring_mesh)This example shows how to create many different complex geometries using Trimesh.
How do I build curves, rings, and other photonic integrated components?
The gdstk library offers a convenient and flexible way to construct commonly used photonic integrated circuit (PIC) components, such as straight waveguides, linear tapers, rings, race tracks, s-bends, circular bends, and directional couplers. This notebook contains pre-defined functions used to construct commonly used PIC components. Users can directly copy these pre-defined functions to their script and use them to build their simulations. More importantly, users can learn the workflow from these examples and create their own Tidy3D structures using the same principles.
How do I build photonic crystal structures?
Tidy3D provides four basic geometric shapes, namely, Box, Cylinder, Sphere, and PolySlab. These shapes can be used to create various periodic structures used in photonic crystals and other photonic devices such as square or hexagonal arrays of cylinders, slabs with square or hexagonal arrays of holes, rectangular grating, L and H cavities, wood pile, and FCC/BCC crystals. For this purpose, you can organize these geometries in a tidy3d.GeometryGroup. This notebook contains functions that can be used to build these popular periodic structures with ease. Moreover, users can learn from these examples and create their own periodic structures using the same principles.
Sources
What source bandwidth should I use for my simulation?
Tidy3D’s broadband source feature is designed to produce the most accurate results in the frequency range of (freq0 - 1.5 * fwidth, freq0 + 1.5 * fwidth). Therefore, it is necessary to define the source center frequency freq0 and bandwidth fwidth to properly cover the desired application frequency range. For example, if the user wants to adjust the source bandwidth to cover a wavelength range between wl_min and wl_max, the source bandwidth can be defined as: fwidth = alpha * (C_0/wl_max - C_0/wl_min), where alpha is a constant typically chosen between 1/3 and 1/2 to ensure accurate results.
How do I set the source frequency and bandwidth?
You can set the source frequency and bandwidth through the source_time parameter, which accepts a tidy3d.GaussianPulse object. In the example below, we create a tidy3d.PointDipole source to radiate power at a center wavelength of 1.55 $\mu$m over a bandwidth of 100 nm.
# Simulation wavelength and bandwidth.
wl = 1.55
bw = 0.1
wl_max = wl + bw / 2
wl_min = wl - bw / 2
freq0 = tidy3d.C_0 / wl
fwidth = 0.5 * (tidy3d.C_0 / wl_min - tidy3d.C_0 / wl_max)
# Source bandwidth.
pulse = tidy3d.GaussianPulse(freq0=freq0, fwidth=fwidth)
# Source definition
pt_dipole = tidy3d.PointDipole(
center=(1,2,3),
source_time=pulse,
polarization='Ex',
interpolate=True,
name="dipole",
)How can I plot the source spectrum and time-dependence?
The tidy3d.GaussianPulse object has the built-in functions plot_spectrum and plot that allow users to visualize the source spectrum and time-dependence, respectively. For example:
# Simulation wavelength and bandwidth.
wl = 1.55
bw = 0.1
wl_max = wl + bw / 2
wl_min = wl - bw / 2
freq0 = td.C_0 / wl
fwidth = 0.5 * (td.C_0 / wl_min - td.C_0 / wl_max)
run_time = 1e-12
# Source bandwidth.
pulse = td.GaussianPulse(freq0=freq0, fwidth=fwidth)
# Source definition
pt_dipole = td.PointDipole(
center=(1,2,3),
source_time=pulse,
polarization='Ex',
interpolate=True,
name="dipole",
)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4), tight_layout=True)
# Plot the source spectrum.
pt_dipole.source_time.plot_spectrum(
times=np.linspace(0, run_time, 2000), val="abs", ax=ax1,
)
# Plot the source time-dependence.
pt_dipole.source_time.plot(
times=np.linspace(0, run_time / 3, 2000), val='real', ax=ax2,
)
plt.show()How can I plot the source spectrum?
When defining a source, you must specify a source time profile, typically Gaussian. For example, we can define a plane wave as
plane_wave = td.PlaneWave(
source_time=td.GaussianPulse(freq0=freq0, fwidth=0.5 * freqw),
size=(td.inf, td.inf, 0),
center=(0, 0, 0.3 * lda0),
direction="-",
pol_angle=0,
)Here, the source time is a Gaussian pulse with central frequency freq0 and frequency width 0.5 * freqw. To visualize the spectrum it gives, we can use the plot_spectrum method by
plane_wave.source_time.plot_spectrum(
times=np.linspace(0, sim.run_time, 2000), val="abs"
)
plt.show()Here, we need to specify the sampled time instances. To ensure the source spectrum is plotted correctly, we need to ensure the time sampling is sufficiently fine and the end time is sufficiently long compared to the pulse width.
How are results normalized?
In many cases, Tidy3D simulations can be run, and well-normalized results can be obtained without normalizing/empty runs. This is because care is taken internally to normalize the injected power, as well as the output results, in a meaningful way. To understand this, there are two separate normalizations that happen, outlined below. Both are discussed with respect to frequency-domain results, as those are the most commonly used.
Source spectrum normalization
Every source has a spectrum associated to its particular time dependence that is imprinted on the fields injected in the simulation. Usually, this is somewhat arbitrary, and it is most convenient to take it out of the frequency-domain results. By default, after a run, Tidy3D normalizes all frequency-domain results by the spectrum of the first
source in the list of sources in the simulation. This choice can be modified using the Simulation.normalize_index attribute, or normalization can be turned off by setting that to None. Results can even be renormalized after the simulation run using SimulationData.renormalize(). If multiple sources are used, but they all have the same time dependence, the default normalization is still meaningful. However, if different sources have a different time dependence, then it may not be
possible to obtain well-normalized results without a normalizing run.
This type of normalization is applied directly to the frequency-domain results. The custom pulse amplitude and phase defined in SourceTime.amplitude and SourceTime.phase, respectively, are not normalized out. This gives the user control over a (complex) prefactor that can be applied to scale any source. Additionally, the power injected by each type of source may have some special normalization, as outlined below.
Source power normalization
Source power normalization is applied depending on the source type. In the cases where normalization is applied, the actual injected power may differ slightly from what is described below due to finite grid effects. The normalization should become exact with sufficiently high resolution. That said, in most cases the error is negligible even at default resolution.
The injected power values described below assume that the source spectrum normalization has also been applied.
-
PointDipole: The point dipole source represents an infinitesimal antenna with a fixed current density. The normalization is such that the power injected by the source in a homogeneous material of refractive index $n$ at frequency $\omega = 2\pi f$ is approximately given as follows
- $\frac{\omega^2}{12\pi}\frac{\mu_0 n}{c}$, 3D simulation, electric current
- $\frac{\omega^2}{12\pi}\frac{\epsilon_0 n^3}{c}$, 3D simulation, magnetic current
- $\frac{\omega \mu_0}{16}$, 2D TE simulation, electric current
- $\frac{\omega \mu_0}{8}$, 2D TM simulation, electric current
- $\frac{\omega \epsilon_0 n^2}{8}$, 2D TE simulation, magnetic current
- $\frac{\omega \epsilon_0 n^2}{16}$, 2D TM simulation, magnetic current
There can be a small difference in the true power compared to the analytical values above due to the finite grid. Note that the current source definition used in Tidy3D is different from the definition of an electric dipole composed of two separated, oscillating electric charges, which is also common. The power normalization differs by a factor of $\omega^2$ for electric dipoles, and $\mu_0^2 \omega^2$ for magnetic dipoles.
-
UniformCurrentSource: No extra normalization applied.
-
CustomFieldSource: No extra normalization applied.
-
ModeSource, PlaneWave, GaussianBeam, AstigmaticGaussianBeam: Normalized to inject 1W power at every frequency. If supplied
SourceTime.num_freqsis1, this normalization is only exact at the central frequency of the associated SourceTime pulse but should still be very close to 1W at nearby frequencies too. Increasingnum_freqscan be used to make sure the normalization works well for a broadband source. The correct usage for a PlaneWave source is to span the whole simulation domain for a simulation with periodic (or Bloch) boundaries, in which case the normalization of this technically infinite source is equivalent to 1W per unit cell. For the other sources which have a finite extent, the normalization is correct provided that the source profile decays by the boundaries of the source plane. Verifying that this is the case is always advised, as otherwise results may be spurious beyond just the normalization (numerical artifacts will be present at the source boundary). -
TFSFSource: Normalized to inject $1W/μm^{2}$ in the direction of the source injection axis. This is convenient for computing scattering and absorption cross-sections without the need for additional normalization. Note that for angled incidence, a factor of $1/\cos(\theta)$ needs to be applied to convert to the power carried by the plane wave in the propagation direction, which is at an angle $\theta$ with respect to the injection axis. Note also that when the source spans the entire simulation domain with periodic or Bloch boundaries, the conversion between the normalization of aTFSFSourceand a PlaneWave is just the area of the simulation domain in the plane normal to the injection axis.
How do I set a PointDipole source?
The tidy3d.PointDipole is a zero-dimensional uniform current source. The example below illustrates how to define tidy3d.PointDipole within a simulation.
# Source bandwidth.
pulse = tidy3d.GaussianPulse(freq0=200e12, fwidth=20e12)
# Source definition
pt_dipole = tidy3d.PointDipole(
center=(1,2,3),
source_time=pulse,
polarization='Ex',
interpolate=True,
name="dipole",
)Use the center parameter to set the dipole position, then adjust the source_time dependence using tidy3d.GaussianPulse. The source polarization defines the direction and type of the current component. Finally, the parameter interpolate handles reverse interpolation of zero-size dimensions of the source. If False, the source data is snapped to the nearest Yee grid point. If True, equivalent source data is applied on the surrounding Yee grid points to emulate placement at the specified location using linear interpolation.
See this notebook to an example on setting up a tidy3d.PointDipole source.
How do I calculate the power radiated by a PointDipole source?
The tidy3d.PointDipole source placed in a lossless homogeneous material injects power close to the analytically expected result for an infinitesimal antenna with oscillating current. There can be a small difference from the analytical result due to the finite grid, which disappears in the limit of high resolution. To calculate the radiated power of a dipole in the presence of dispersive, lossy, or non-homogeneous materials, you can use a tidy3d.FluxMonitor box. Refer to this notebook for an example.
How do I set a UniformCurrentSource source?
The tidy3d.UniformCurrentSource is a rectangular volume source with uniform time dependence. The example below illustrates how to define a tidy3d.UniformCurrentSource within a simulation.
# Source bandwidth.
pulse = tidy3d.GaussianPulse(freq0=200e12, fwidth=20e12)
# Source definition
source = tidy3d.UniformCurrentSource(
center=(1,2,3),
size=(0,2,1),
source_time=pulse,
polarization='Ex',
interpolate=True,
name="uniform_source",
)Use the center and size parameters to set the source position and volume, then adjust the source_time dependence using tidy3d.GaussianPulse. The source polarization defines the direction and type of the current component. Finally, the parameter interpolate handles reverse interpolation of zero-size dimensions of the source. If False, the source data is snapped to the nearest Yee grid point. If True, equivalent source data is applied on the surrounding Yee grid points to emulate placement at the specified location using linear interpolation. Note that making size=(0, 0, 0) is equivalent to including a tidy3d.PointDipole source.
How do I set a PlaneWave source?
The tidy3d.PlaneWave is a uniform current distribution on an infinite extent plane. The example below illustrates how to define a tidy3d.PlaneWave within a simulation.
# Source bandwidth.
pulse = tidy3d.GaussianPulse(freq0=200e12, fwidth=20e12)
# Source definition
source = tidy3d.PlaneWave(
center=(0, 0, 5),
size=(tidy3d.inf, tidy3d.inf, 0),
source_time=pulse,
direction='-',
pol_angle=np.pi/2,
angle_theta=0,
angle_phi=0,
name="plane_wave",
)Use the center and size parameters to set the source position and dimension, then adjust the source_time dependence using tidy3d.GaussianPulse. The direction parameter specifies propagation in the positive or negative direction of the injection axis. You can change the light polarization using pol_angle, and adjust the propagation axis direction with angle_theta and angle_phito control the polar and azimuth angles.
This example illustrates setting up a tidy3d.PlaneWave source at normal and off-normal incidences.
How do I set a ModeSource?
The tidy3d.ModeSource injects a current source in the simulation to excite a modal profile in a finite extent plane. It is commonly used to excite specific waveguide modes in photonic integrated circuits. To illustrate how to set up a tidy3d.ModeSource, let’s consider the case of injecting the first-order transverse electric (TE) mode in a silicon-on-insulator (SOI) waveguide operating at 1.55 $\mu$m.
# Source bandwidth.
pulse = tidy3d.GaussianPulse(freq0=1.934e14, fwidth=6.245e12)
# Mode specification.
mode_spec = tidy3d.ModeSpec(target_neff=3.47, filter_pol='te', num_modes = 2)
# Source definition
source = tidy3d.ModeSource(
center=(0, 0, -2),
size=(0, 2, 1.5),
source_time=pulse,
direction='+',
mode_spec=mode_spec,
mode_index=1,
name="mode_source",
)You should use the center and size parameters to define a source plane surrounding the waveguide, then adjust the source_time dependence using tidy3d.GaussianPulse. The direction='+' parameter specifies propagation in the positive waveguide axis. The tidy3d.ModeSpec object includes all the specifications of a mode solver, which calculates the optical modes given the material distribution within the source plane. The modes calculated by the mode solver are sorted by their effective indices in descending order. So, we have set the initial mode solver guess to the core refractive index (target_neff=3.47) and chosen filter_pol='te' to make sure it will return first in the list of the TE waveguide modes, starting from the fundamental one. Finally, to inject the first-order TE mode in the waveguide, we setmode_index=1`.
This example illustrates setting up a tidy3d.ModeSource source.
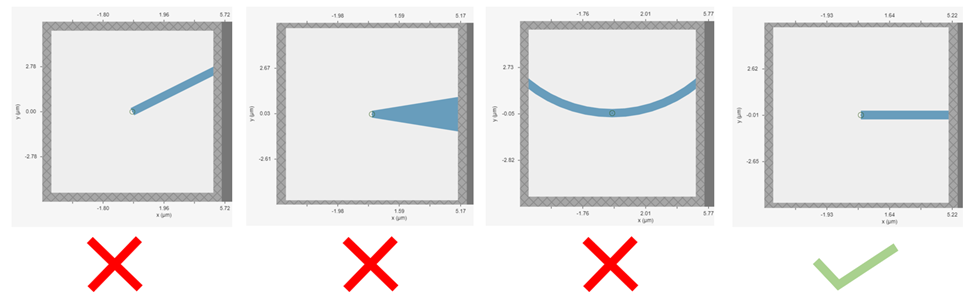
How do I inject a specific optical mode in a waveguide?
To inject a specific optical mode in the waveguide, you can use the tidy3d.ModeSource source. Let’s consider the case of injecting the first-order transverse electric (TE) mode in a silicon-on-insulator (SOI) waveguide operating at 1.55 $\mu$m as an example:
# Source bandwidth.
pulse = tidy3d.GaussianPulse(freq0=1.934e14, fwidth=6.245e12)
# Mode specification.
mode_spec = tidy3d.ModeSpec(target_neff=3.47, filter_pol='te', num_modes = 2)
# Source definition
source = tidy3d.ModeSource(
center=(0, 0, -2),
size=(0, 2, 1.5),
source_time=pulse,
direction='+',
mode_spec=mode_spec,
mode_index=1,
name="mode_source",
)You should use the center and size parameters to define a source plane surrounding the waveguide, then adjust the source_time dependence using tidy3d.GaussianPulse. The direction='+' parameter specifies propagation in the positive waveguide axis. The tidy3d.ModeSpec object includes all the specifications of a mode solver, which calculates the optical modes given the material distribution within the source plane. The modes calculated by the mode solver are sorted by their effective indices in descending order. So, we have set the initial mode solver guess to the core refractive index (target_neff=3.47) and chosen filter_pol='te' to make sure it will return first in the list of the TE waveguide modes, starting from the fundamental one. Finally, to inject the first-order TE mode in the waveguide, we set mode_index=1.
This example illustrates setting up a tidy3d.ModeSource source.
How do I inject an optical mode in a waveguide bend?
To inject an optical mode in a waveguide bend, you must set the bend_radius and bend_axis parameters of tidy3d.ModeSpec. For example:
# Source bandwidth.
pulse = tidy3d.GaussianPulse(freq0=1.934e14, fwidth=6.245e12)
# Mode specification.
mode_spec = tidy3d.ModeSpec(target_neff=2.5, bend_radius=-5, bend_axis=1)
# Source definition
source = tidy3d.ModeSource(
center=(0, 0, -2),
size=(0, 2, 1.5),
source_time=pulse,
direction='+',
mode_spec=mode_spec,
mode_index=0,
name="mode_source",
)You can find a detailed example in this notebook.
How do I set a GaussianBeam?
The source tidy3d.GaussianBeam is a Guassian distribution on a finite extent plane. The example below illustrates how to define the tidy3d.GaussianBeam within a simulation.
# Source bandwidth.
pulse = tidy3d.GaussianPulse(freq0=200e12, fwidth=20e12)
# Source definition
gauss_source = tidy3d.GaussianBeam(
center=(0, -5, 0),
size=(0, 3, 3),
source_time=pulse,
direction='+',
pol_angle=0,
angle_theta=0,
angle_phi=0,
waist_radius=1.0,
waist_distance=-2.5,
name="gauss_source",
)Use the center and size parameters to set the source position and dimension, then adjust the source_time dependence using tidy3d.GaussianPulse. The direction parameter specifies propagation in the positive or negative direction of the injection axis. You can change the light polarization using pol_angle, and adjust the propagation axis direction with angle_theta and angle_phito control the polar and azimuth angles. In this example, the beam’s radius at the waist position was adjusted to 1$\mu$m using the waist_radius parameter. When waist_distance is positive (negative), the waist is behind (front) the source plane.
See this notebook to an example on setting up a tidy3d.GaussianBeam source.
How do I model an optical fiber mode source?
To simulate an optical fiber mode source, you can use the tidy3d.ModeSource. This object allows you to solve for the optical modes of a fiber cross-section. You can then include this in your simulation by following the steps outlined in the example.
If you prefer, you can also use the tidy3d.GaussianBeam source instead to approximate the optical mode of the fiber with a Gaussian distribution, as explained in more detail in another example.
How do I model a converging Gaussian beam?
To create a converging Gaussian beam, include a tidy3d.GaussianBeam source in the simulation, and set the waist_distance to negative values. This way, the beam waist will lie in the front of the source plane, as illustrated in the following example
# Source bandwidth.
pulse = tidy3d.GaussianPulse(freq0=200e12, fwidth=20e12)
# Source definition
gauss_source = tidy3d.GaussianBeam(
center=(0, -5, 0),
size=(0, 3, 3),
source_time=pulse,
direction='+',
pol_angle=0,
angle_theta=0,
angle_phi=0,
waist_radius=1.0,
waist_distance=-2.5,
name="gauss_source",
)See this notebook to an example on setting up a tidy3d.GaussianBeam source.
How do I model a diverging Gaussian beam?
To create a diverging Gaussian beam, include a tidy3d.GaussianBeam source in the simulation, and set them waist_distance to positive values. This way, the beam waist will lie behind the source plane, as illustrated in the following example
# Source bandwidth.
pulse = tidy3d.GaussianPulse(freq0=200e12, fwidth=20e12)
# Source definition
gauss_source = tidy3d.GaussianBeam(
center=(0, -5, 0),
size=(0, 3, 3),
source_time=pulse,
direction='+',
pol_angle=0,
angle_theta=0,
angle_phi=0,
waist_radius=1.0,
waist_distance=2.5,
name="gauss_source",
)See this notebook to an example on setting up a tidy3d.GaussianBeam source.
How do I set an AstigmaticGaussianBeam source?
The tidy3d.AstigmaticGaussianBeam class implements the simple astigmatic Gaussian beam described in Kochkina et al., Applied Optics, vol. 52, issue 24, (2013). The simple astigmatic Guassian distribution allows both an elliptical intensity profile and different waist locations for the two principal axes of the ellipse. The following example illustrates how to set up a tidy3d.AstigmaticGaussianBeam.
# Source bandwidth.
pulse = tidy3d.GaussianPulse(freq0=200e12, fwidth=20e12)
# Source definition
gauss_source = tidy3d.AstigmaticGaussianBeam(
center=(0, -5, 0),
size=(0, 3, 3),
source_time=pulse,
direction='+',
pol_angle=0,
angle_theta=0,
angle_phi=0,
waist_sizes=(1.0, 2.0),
waist_distances=(-1.0, -2.0),
name="gauss_source",
)Use the center and size parameters to set the source position and dimension, then adjust the source_time dependence using tidy3d.GaussianPulse. The direction parameter specifies propagation in the positive or negative direction of the injection axis. You can change the light polarization using pol_angle, and adjust the propagation axis direction with angle_theta and angle_phi to control the polar and azimuth angles. In this example, different waist_sizes and waist_distances were specified in the x- and y-directions.
How do I set a total-field scattered-field (TFSF) source?
The total-field scattered-field (TFSF) source injects a plane wave in a finite region. The example below illustrates how to define the tidy3d.TFSF within a simulation.
# Source bandwidth.
pulse = tidy3d.GaussianPulse(freq0=200e12, fwidth=20e12)
# Source definition
tfsf_source = tidy3d.TFSF(
center=(0, 0, 5),
size=(3, 3, 0),
source_time=pulse,
direction='-',
pol_angle=np.pi / 2,
angle_theta=np.pi / 4,
angle_phi=0,
injection_axis=2,
name="tfsf_source",
)Use the center and size parameters to set the source position and dimension, then adjust the source_time dependence using tidy3d.GaussianPulse. The direction parameter specifies propagation in the positive or negative direction of the injection axis. You can change the light polarization using pol_angle, and adjust the propagation axis direction with angle_theta and angle_phito control the polar and azimuth angles. The injection_axis parameter specifies injection along the x (0), y (1), or z (2) direction.
See this notebook to an example on setting up a tidy3d.TFSF source.
How do I set a custom field source?
The tidy3d.CustomFieldSource source can be used to inject a specific (E, H) field distribution on a plane, e.g. coming from another simulation. Internally, we use the equivalence principle to compute the actual source currents (all sources in FDTD have to be converted to current sources). Because of this, the custom field source will only produce reliable results if the provided fields decay by the edges of the source plane, or if they extend through the simulation boundaries and are well-matched to those boundaries.
The example below illustrates how to define the tidy3d.CustomFieldSource using a dataset containing the E and H fields to describe a Gaussian field profile.
# Source bandwidth.
pulse = tidy3d.GaussianPulse(freq0=200e12, fwidth=20e12)
# Scalar gaussian field.
waist_radius = 2
ys, zs = np.linspace(-4, 4, 101), np.linspace(-4, 4, 101)
y_grid, z_grid = np.meshgrid(ys, zs)
scalar_gaussian = np.exp(-(y_grid**2 + z_grid**2) / waist_radius**2)
# Field dataset defining both E and H
dataset_EH = tidy3d.FieldDataset(
Ey=tidy3d.ScalarFieldDataArray(
scalar_gaussian[None, ..., None],
coords={
"x": [0],
"y": ys,
"z": zs,
"f": [200e12],
},
),
Hz=tidy3d.ScalarFieldDataArray(
scalar_gaussian[None, ..., None] / td.ETA_0,
coords={
"x": [0],
"y": ys,
"z": zs,
"f": [200e12],
},
),
)
# Source definition
custom_field_src = tidy3d.CustomFieldSource(
source_time=pulse,
center=(-1, 1, 0),
size=(0, 8, 8),
field_dataset=dataset_EH,
)See this notebook to an example on setting up a tidy3d.CustomFieldSource source.
How do I set a custom current source?
The tidy3d.CustomCurrentSource source can be used to inject a raw electric and magnetic current distribution within the simulation. Its syntax is very similar to that of CustomFieldSource, except the source accepts a current_dataset instead of a field_dataset, and it can be volumetric or planar without requiring tangential components. This dataset still contains the E{x,y,z} and H{x,y,z} field components, which correspond to J and M components, respectively.
See this notebook to an example on setting up a tidy3d.CustomCurrentSource source.
How do I inject an optical mode in an angled waveguide?
To inject an optical mode in an angled waveguide, you must set the angle_theta and angle_phi parameters of tidy3d.ModeSpec. For example:
# Source bandwidth.
pulse = tidy3d.GaussianPulse(freq0=1.934e14, fwidth=6.245e12)
# Mode specification.
mode_spec = tidy3d.ModeSpec(target_neff=2.5, angle_theta=1.5, angle_phi=0)
# Source definition
source = tidy3d.ModeSource(
center=(0, 0, -2),
size=(0, 2, 1.5),
source_time=pulse,
direction='+',
mode_spec=mode_spec,
mode_index=0,
name="mode_source",
)You can find a detailed example in this notebook.
Grid Specification
What do I need to know about the numerical grid?
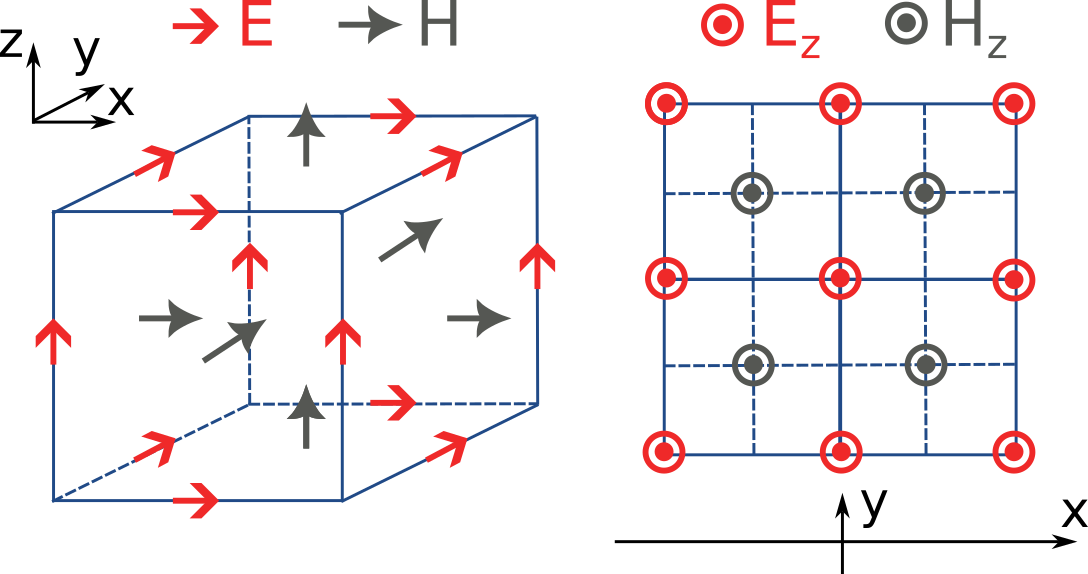
Tidy3D tries to provide an illusion of continuity as much as possible, but at the level of the solver, a finite numerical grid is used, which can have some implications that advanced users may want to be aware of.
The FDTD method for electromagnetic simulations uses what is called the Yee grid, in which every field component is defined at a different spatial location, as illustrated in the figure, as well as in our FDTD video tutorial FDTD 101 videos. On the left, we show one cell of the full 3D Yee grid and where the various E and H field components live. On the right, we show a cross-section in the xy plane and the locations of the Ez and Hz field components in that plane (note that these field components are not in the same cross-section along z but rather also offset by half a cell size). This illustrates a duality between the grids on which E and H fields live, which is related to the duality between the fields themselves. There is a primal grid, shown with solid lines, and a dual grid, shown with dashed lines, with the Ez and Hz fields living at the primal/dual vertices in the xy-palne, respectively. In some literature on the FDTD method, the primal and dual grids may even be switched as the definitions are interchangeable. In Tidy3D, the primal grid is as defined by the solid lines in the Figure.
When computing results that involve multiple field components, like Poynting vector, flux, or total field intensity, it is important to use fields that are defined at the same locations for best numerical accuracy. The field components thus need to be interpolated, or colocated, to some common coordinates. All this is already done under the hood when using Tidy3D in-built methods to compute such quantities. When using field data directly, Tidy3D provides several conveniences to handle this. Firstly, field monitors have a colocate option, set to True by default, which will automatically return the field data interpolated to the primal grid vertices. The data is then ready to be used directly for computing quantities derived from any combination of the field components. The colocate option can be turned off by advanced users, in which case each field component will have different coordinates as defined by the Yee grid. In some cases, this can lead to more accurate results, as discussed, for example, in the custom source
example. In that example, when using data generated by one simulation as a source in another, it is best to use the fields as recorded on the Yee grid.
Regardless of whether the colocate option is on or off for a given monitor, the data can also be easily colocated after the solver run. In principle, if colocating to locations other than the primal grid in post-processing, it is more accurate to set colocate=False in the monitor to avoid double interpolation (first to the primal grid in the
solver, then to new locations). Regardless, the following methods work for both Yee grid data and data that has already been previously colocated:
-
data_at_boundaries = sim_data.at_boundaries(monitor_name)to colocate all fields of a monitor to the Yee grid cell boundaries (i.e. the primal grid vertexes). -
data_at_centers = sim_data.at_centers(monitor_name)to colocate all fields of a monitor to the Yee grid cell centers (i.e. the dual grid vertexes). -
data_at_coords = sim_data[monitor_name].colocate(x=x_points, y=y_points, z=z_points)to colocate all fields to a custom set of coordinates. Any or all ofx,y, andzcan be supplied; if some are not, the original data coordinates are kept along that dimension.
How fine of a grid or mesh does my simulation need? How to choose grid spec?
The FDTD and other similar numerical methods will always give approximate results for a set of finite-difference equations. The accuracy of Maxwell’s equations solution for any geometry can be arbitrarily increased by using smaller and smaller values of the space and time increments. This strategy often involves increased simulation time and memory, so it is essential to consider, for your application, the desired accuracy in results so that you can run your simulations as quickly as possible. As a gold rule of thumb, ten grid points per wavelength in the highest refractive index medium should be a good starting value for the grid resolution. However, other application specificities must be considered when defining the appropriate simulation mesh, such as very thin geometries or large electric field gradients, as usually occurs, for example, in the presence of resonances, highly confined fields, or at metal-dielectric interfaces.
Tidy3D has many features that give users a simple and flexible way to build the simulation mesh. The GridSpec object enables the user to chose between an AutoGrid, a UniformGrid, or a CustomGrid, at each of the simulation x-, y-, z-direction. An example code snippet is shown below:
uniform = tidy3d.UniformGrid(dl=0.1)
custom = tidy3d.CustomGrid(dl=[0.2, 0.2, 0.1, 0.1, 0.1, 0.2, 0.2])
auto = tidy3d.AutoGrid(min_steps_per_wvl=12)
grid_spec = tidy3d.GridSpec(grid_x=uniform, grid_y=custom, grid_z=auto, wavelength=1.5)More examples of setting up the simulation mesh are available on this notebook.
In general, a good strategy is to start with the default object AutoGrid to discretize the whole simulation domain and fine-tune the mesh by increasing the grid resolution at directions or regions containing smallest geometric features or high field gradients or even relaxing the discretization along directions of invariant geometry, e.g., the propagation direction of channel waveguides. The definition of an override structure is an efficient way to improve simulation accuracy while keeping the run time small.
How to use the automatic nonuniform meshing? What steps per wavelength will be sufficient?
By default, Tidy3D configures the GridSpec object to having AutoGrid, which is an advanced meshing algorithm to automatically define a nonuniform grid in all three domain directions. The resolution of this grid is specified using the desired minimum steps per wavelength in each material (min_steps_per_wvl = 10 by default). This specification, therefore, requires a target wavelength, which can be provided directly to grid_spec or inferred from any sources present in the simulation. Detailed examples on how to set up AutoGrid are present on this notebook.
As a gold rule of thumb, the default value of 10 grid points per wavelength should be a good starting value for min_steps_per_wvl. However, other application-specific features must be considered when defining the appropriate simulation mesh, such as very thin geometries or large electric field gradients, as can usually occur, for example, in the presence of resonances, highly confined fields, or at metal-dielectric interfaces. Additional control over the mesh is obtained by the dl_min parameter, which imposes a lower bound of the grid size regardless of the structures present in the simulation, including override structures with enforced=True. This is, however, a soft bound, meaning that the actual minimal grid size might be slightly smaller. Finally, the max_scale sets the maximum ratio between two consecutive grid steps. Different grid configurations can be chosen for each direction, as illustrated below:
grid_spec = td.GridSpec(
grid_x=td.AutoGrid(min_steps_per_wvl=20,dl_min=0.01),
grid_y=td.AutoGrid(min_steps_per_wvl=15),
grid_z=td.AutoGrid(min_steps_per_wvl=10,max_scale=1.6),
wavelength=1.0,
)How can I create a uniform grid?
The most standard way to define a simulation is to use a constant grid size in each of the three directions. This can be achieved simply using tidy3d.GridSpec.uniform(dl=...) as shown below.
# Setting a uniform grid size of 0.02 microns.
sim_uniform = tidy3d.Simulation(
size=(5, 5, 5),
grid_spec=tidy3d.GridSpec.uniform(dl=0.02),
medium=tidy3d.Medium(permittivity=4),
structures=[structure],
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=td.PML())
run_time=1e-12,
)How can I locally refine the mesh?
In some problems, the user may want to refine the grid mesh locally around specific geometry features, such as the gap between two very close waveguides where we expect the fields to be strongest. This can be achieved by adding override_structures to the simulation grid_spec. The override structures is a list of Tidy3D structures, each with an arbitrary geometry, used exclusively for the meshing. It is added on top of any physical simulation structures. There are two types of Tidy3D structures that can be added to override_structures list. The first type defines a fictitious medium inside the override structure so that the grid size is decided by the minimum steps per wavelength in the medium. The second type is more straightforward: one can directly define the grid size along each axis inside the override structures.
Fictitious Medium
The first type is identical to the Structure object that consists of a Geometry and a Medium. The grid step in the override_structure region is decided by the minimum steps per wavelength in this medium.
# Define a "dummy" box with a refractive index 5 around the central location of a slot waveguide.
refine_box = tidy3d.Structure(
geometry=tidy3d.Box(center=(0, 0, 0), size=(td.inf, 0.4, 0.4)),
medium=tidy3d.Medium(permittivity=5**2),
)
# Use the box as a grid refinement structure.
sim_refined = tidy3d.Simulation(
size=[5, 3, 3],
grid_spec=tidy3d.GridSpec.auto(
wavelength=1.55,
min_steps_per_wvl=20,
override_structures=[refine_box],
),
medium=tidy3d.Medium(permittivity=1.44**2),
structures=[wave_guide_1, wave_guide_2],
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML()),
run_time=1e-12,
)Override Structure
The second type is the tidy3d.MeshOverrideStructure object that consists of a Geometry, and a tuple dl specifying the grid sizes along x, y, and z-directions. We can override the grid sizes just along a few selected directions by setting the value to be None in the dl tuple along the other directions. E.g., if we only plan to refine the grid size along x-direction with grid size 0.01 $\mu$m, we can apply dl=(0.01, None, None). In the following, we override the grid size along y and z to be 15.5nm.
# Define a MeshOverrideStructure.
refine_box = tidy3d.MeshOverrideStructure(
geometry=tidy3d.Box(center=(0, 0, 0), size=(td.inf, 0.4, 0.4)),
dl=[None, 0.015, 0.015],
)
# Use the box as a grid refinement structure.
sim_refined = tidy3d.Simulation(
size=[5, 3, 3],
grid_spec=tidy3d.GridSpec.auto(
wavelength=1.55,
min_steps_per_wvl=20,
override_structures=[refine_box],
),
medium=tidy3d.Medium(permittivity=1.44**2),
structures=[wave_guide_1, wave_guide_2],
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML()),
run_time=1e-12,
)Boundary Conditions
Which types of boundary conditions are available in Tidy3D?
Tidy3D includes the following boundary condition types: Periodic, PECBoundary, PMCBoundary, BlochBoundary, PML, StablePML, and Absorber.
How do I set the perfect matched layer (PML) boundary condition?
You should use tidy3d.PML boundary condition to enclose the simulation domain with layers of a special lossy material designed to absorb incoming waves from all angles with minimal reflection. Tidy3D uses PML boundary conditions by default, but you can also set the boundaries explicitly using the all_sides() method. For example:
# Define PML boundary conditions in all sides.
bspec = tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML())
# Alternatively, you can apply the boundary at specific directions.
# bspec = tidy3d.BoundarySpec.pml(x=True, y=True)
# Build the simulation.
sim = tidy3d.Simulation(
center=(0, 0, 0),
size=(10, 4, 4),
boundary_spec=bspec,
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
sources=[mode_source],
monitors=[mode_monitor],
run_time=1e-12,
)See this notebook for more details on setting up boundary conditions.
How do I set the perfect electric conductor (PEC) boundary condition?
You should use tidy3d.PECBoundary to enclose the simulation domain using perfect electric conductors. For example:
# Define PML boundary conditions in all sides.
bspec = tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PECBoundary())
# Alternatively, you can apply the boundary at specific directions.
# bspec = tidy3d.BoundarySpec.pec(x=True, y=True)
# Build the simulation.
sim = tidy3d.Simulation(
center=(0, 0, 0),
size=(10, 4, 4),
boundary_spec=bspec,
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
sources=[mode_source],
monitors=[mode_monitor],
run_time=1e-12,
)See this notebook for more details on setting up boundary conditions.
How do I set the perfect magnetic conductor (PMC) boundary condition?
You should use tidy3d.PMCBoundary to enclose the simulation domain using perfect magnetic conductors. For example:
# Define PML boundary conditions in all sides.
bspec = tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PMCBoundary())
# Alternatively, you can apply the boundary at specific directions.
# bspec = tidy3d.BoundarySpec.pmc(x=True, y=True)
# Build the simulation.
sim = tidy3d.Simulation(
center=(0, 0, 0),
size=(10, 4, 4),
boundary_spec=bspec,
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
sources=[mode_source],
monitors=[mode_monitor],
run_time=1e-12,
)See this notebook for more details on setting up boundary conditions.
How do I set the periodic boundary condition?
# Definition of periodic boundary condition in the x and y directions.
# PML in the z-direction.
bspec = tidy3d.BoundarySpec(
x=tidy3d.Boundary(minus=tidy3d.Periodic(), plus=tidy3d.Periodic()),
y=tidy3d.Boundary(minus=tidy3d.Periodic(), plus=tidy3d.Periodic()),
z=tidy3d.Boundary(minus=tidy3d.PML(), plus=tidy3d.PML()),
)
# Build the simulation.
sim = tidy3d.Simulation(
center=(0, 0, 0),
size=(2, 2, 10),
boundary_spec=bspec,
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[unit_cell],
sources=[plane_wave],
monitors=[flux_monitor],
run_time=1e-12,
)Details about the periodic boundary condition
x-direction along a periodic structure with period $L_x$, they must satisfy:x-direction.See this notebook for more details on setting up boundary conditions.
How do I set the Bloch boundary condition?
# Simulation size.
sim_size = (2, 2, 8)
# Plane wave source at an angle.
plane_wave = tidy3d.PlaneWave(
center=(0, 0, 3),
size=(tidy3d.inf, tidy3d.inf, 0),
source_time=source_time,
direction="-",
pol_angle=0,
angle_theta=np.pi / 3.0,
angle_phi=np.pi / 6.0,
)
# Bloch boundaries.
bloch_x = tidy3d.Boundary.bloch_from_source(
source=plane_wave,
domain_size=sim_size[0],
axis=0,
medium=medium
)
bloch_y = tidy3d.Boundary.bloch_from_source(
source=plane_wave,
domain_size=sim_size[1],
axis=1,
medium=medium
)
bspec = tidy3d.BoundarySpec(x=bloch_x, y=bloch_y, z=tidy3d.Boundary.pml())
# Build the simulation.
sim = tidy3d.Simulation(
center=(0, 0, 0),
size=sim_size,
boundary_spec=bspec,
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[unit_cell],
sources=[plane_wave],
monitors=[flux_monitor],
run_time=1e-12,
)source, background medium, axis, and domain_size information.See this notebook for more details on setting up boundary conditions.
How do I set the Absorber boundary condition?
The tidy3d.Absorber boundary condition specifies an adiabatic absorber along a single dimension. This absorber is well-suited for dispersive materials intersecting with absorbing edges of the simulation at the expense of more layers. The example below shows how to set up an absorbing boundary.
# Define PML boundary conditions in all sides.
bspec = tidy3d.BoundarySpec.all_sides(boundary=tidy3d.Absorber(num_layers=40))
# Build the simulation.
sim = tidy3d.Simulation(
center=(0, 0, 0),
size=(10, 4, 4),
boundary_spec=bspec,
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
sources=[mode_source],
monitors=[mode_monitor],
run_time=1e-12,
)See this notebook for more details on setting up boundary conditions.
How do I specify different boundary conditions on each simulation domain edge?
# Definition different boundary conditions.
bspec = tidy3d.BoundarySpec(
x=tidy3d.Boundary(minus=tidy3d.PECBoundary(), plus=tidy3d.PECBoundary()),
y=tidy3d.Boundary(minus=tidy3d.Periodic(), plus=tidy3d.Periodic()),
z=tidy3d.Boundary(minus=tidy3d.PML(), plus=tidy3d.PMCBoundary()),
)
# Build the simulation.
sim = tidy3d.Simulation(
center=(0, 0, 0),
size=(2, 2, 10),
boundary_spec=bspec,
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[unit_cell],
sources=[plane_wave],
monitors=[flux_monitor],
run_time=1e-12,
)See this notebook for more details on setting up boundary conditions.
Can my geometry lie within the boundary layers?
Structures can indeed be larger than the simulation domain in Tidy3D. In such cases, Tidy3D will automatically truncate the geometry that goes beyond the domain boundaries. For best results, structures that intersect with absorbing boundaries or simulation edges should extend all the way through. In many such cases, an “infinite” size tidy3d.inf can be used to define the size along that dimension.
It is essential to keep in mind that PML only absorbs propagating fields. For evanescent fields, PML can act as an amplification medium and cause a simulation to diverge. In Tidy3D, a warning will appear if the distance between a structure is smaller than half of a wavelength to prevent evanescent fields from leaking into PML. In most cases, the evanescent field will naturally die off within half a wavelength, but in some instances, a larger distance may be required.
What is the ideal distance between the geometry and absorbing layers?
In Tidy3D, a warning will appear if the distance between a structure and the absorbing layers is smaller than half of a wavelength to prevent evanescent fields from leaking into PML. In most cases, the evanescent field will naturally die off within half a wavelength, but in some instances, a larger distance may be required. It is important to keep in mind that PML only absorbs propagating fields. PML can act as an amplification medium for evanescent fields and cause a simulation to diverge.
How do I avoid reflections from the simulation edges?
You should use tidy3d.PML boundary condition to enclose the simulation domain with layers of a special lossy material designed to absorb incoming waves from all angles with minimal reflection. Tidy3D uses PML boundary conditions by default, but you can also set the boundaries explicitly using the all_sides() method. For example:
# Define PML boundary conditions in all sides.
bspec = tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML())
# Alternatively, you can apply the boundary at specific directions.
# bspec = tidy3d.BoundarySpec.pml(x=True, y=True)
# Build the simulation.
sim = tidy3d.Simulation(
center=(0, 0, 0),
size=(10, 4, 4),
boundary_spec=bspec,
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
sources=[mode_source],
monitors=[mode_monitor],
run_time=1e-12,
)In some cases, such as when an angled structure or dispersive materials lie within the PML, use tidy3d.Absorber instead. The absorber functions similarly to PML, absorbing the outgoing radiation to mimic the infinite space. However, the absorber has a slightly higher reflection and requires a bit more computation than PML, but it is numerically much more stable.
See this notebook for more details on setting up boundary conditions.
How do I simulate periodic structures in Tidy3D?
See this notebook for more details on setting up boundary conditions.
What is The Difference Between Periodic and Bloch Boundaries?
Periodic and Bloch boundary conditions are very useful for simulating periodic structures. When using Periodic boundary conditions, the fields are registered on one edge of the simulation domain and re-injected at the opposite edge. Bloch boundary conditions are similar, but they also apply a phase correction term to the fields. In other words, Periodic boundary conditions can be considered a special case of Bloch boundaries. When a normal incident plane wave is considered, there will not be any difference between them. However, if we consider a plane wave propagating at an angle, the fields from one period to the next will not be exactly periodic and will be out of phase by some amount. The Bloch boundary condition corrects this factor. Therefore, when injecting plane waves at an angle, Bloch boundaries should be used.
Symmetry
Why is it preferable to use symmetry whenever possible?
In many Tidy3D simulations, the application of field symmetries can markedly decrease computational time and FlexCredit cost, potentially achieving reductions by factors of 1/2, 1/4, or even 1/8. Therefore, we prefer to use symmetry whenever applicable. In addition, symmetry effectively filters out unwanted light polarizations or modes.
However, correctly setting up the symmetry is essential to avoid getting incorrect results. For a more extensive discussion on symmetry, please visit the dedicated tutorial.
How do I set symmetry in Tidy3D?
To configure symmetry in your simulation, assign a tuple of integers to the symmetry parameter. This tuple defines the reflection symmetry across planes bisecting the simulation domain normal to the x-, y-, and z-axes. Each element of the tuple can be set to 0 for no symmetry, 1 for even symmetry (equivalent to ‘PMC’ symmetry), or -1 for odd symmetry (equivalent to ‘PEC’ symmetry). For example,
# Define the symmetry tuple
symmetry_tuple = (0, 1, -1)
# Build the simulation.
sim = td.Simulation(
center=(0, 0, 0),
size=(10, 4, 4),
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=td.PML()),
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
sources=[mode_source],
monitors=[mode_monitor],
run_time=1e-12,
symmetry=symmetry_tuple,
)It is crucial to consider the vectorial nature of the electromagnetic fields when determining the appropriate symmetry value. For a more extensive discussion on symmetry, please visit the dedicated tutorial.
How do I identify the symmetry planes of my simulation?
To identify the symmetry planes in your simulation, the first step is to look for reflection symmetries in the geometry as well as the sources of your setup. If your entire simulation setup has reflection symmetry with respect to the x=0 plane, then symmetry can be applied to the x-direction. Same for the y- and z-directions. This only determines if symmetry exists but doesn’t tell us what type (even or odd) of symmetry should be applied.
Once we identify the existence of symmetry in a direction, we need to evaluate the source field. When symmetry exists, certain field components are necessarily zero at the plane of symmetry. PMC symmetry (even) corresponds to zero normal electric field and zero tangential magnetic field at the symmetry plane. PEC symmetry (odd) corresponds to zero tangential electric fields and zero normal magnetic fields at the symmetry plane. Another rule of thumb is to check if the electric field created by the source is perpendicular to the symmetry plane (odd symmetry) or parallel to the symmetry plane (even symmetry).
For example, a plane wave polarized in the y-direction propagating in the z-direction has symmetry (1, -1, 0) since the electric field is parallel to the x=0 plane and perpendicular to the y=0 plane.
For a more extensive discussion on symmetry, please visit the dedicated tutorial.
What does “odd, i.e. ‘PEC’ symmetry” mean?
PEC symmetry (odd) corresponds to zero tangential electric fields and zero normal magnetic fields at the symmetry plane.
What does “even, i.e. ‘PMC’ symmetry” mean?
PMC symmetry (even) corresponds to zero normal electric field and zero tangential magnetic field at the symmetry plane.
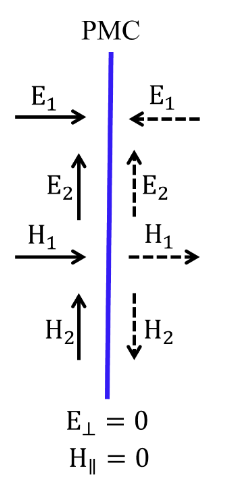
How do I filter out waveguide modes using symmetry?
Different waveguide modes process different symmetries. When we define the symmetry for the simulation, only the waveguide modes with the same symmetry can be found at the mode sources and monitors.
For example, for a rectangular strip waveguide buried in oxide with a mode source propagating in the y direction, as shown below, we can identify two symmetry planes at x=0 and z=0. All TE modes with electric fields predominantly in the x direction have symmetry (0,0,1), while all TM modes have symmetry (0,0,-1). Furthermore, even TE modes (TE0, TE2, TE4, …) have symmetry (-1,0,1) while odd TE modes (TE1, TE3, TE5, …) have symmetry (1,0,1). Even TM modes (TM0, TM2, TM4, ..) have symmetry (1,0,-1) while odd TM modes (TM1, TM3, TM5, ..) have symmetry (-1,0,-1). Therefore, by using certain symmetry, we can selectively filter out waveguide modes. Note that when the cladding and substrate materials are different or the waveguide has a nonzero sidewall angle, certain symmetry will be broken.
For a more extensive discussion on waveguide mode filtering using symmetry, please visit the dedicated tutorial.
Does Tidy3D support continuous and discrete rotational symmetries?
At the moment, Tidy3D does not support continuous and discrete rotational symmetries. Only mirror symmetries are supported. For more information on using symmetry to significantly reduce simulation time and cost, please refer to the tutorial Defining and using symmetries tutorial.
Mode Solver
How do I set the mode solver?
# Define the waveguide.
waveguide = tidy3d.Structure(
geometry=tidy3d.Box(size=(tidy3d.inf, 0.5, 0.22)),
medium=tidy3d.Medium(permittivity=3.47**2),
)
# Build a simulation object including the waveguide.
sim = tidy3d.Simulation(
size=(10, 2.5, 1.5),
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
run_time=1e-12,
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML()),
)You can use a Box object to define the plane where you want to solve the modes. In this example, we use a plane perpendicular to the waveguide propagation axis. Symmetries are applied if they are defined in the simulation and the mode plane center sits on the simulation center. Then, use the tidy3d.ModeSpec object to specify the number of modes (num_modes), the initial effective index guess (target_neff), polarization, and other characteristics of the modes you are looking for. Make group_index_step=True to enable mode group index calculation.
# Plane we want to solve the modes.
plane = tidy3d.Box(center=(0, 0, 0), size=(0, 2.5, 1.5))
# Mode specification.
mode_spec = tidy3d.ModeSpec(
num_modes=4,
target_neff=3.47,
group_index_step=True,
)Now you can create and execute the mode solver, which returns the results in a ModeSolverData object. For more details on how to set up, run, and visualize the solver results, please refer to this notebook.
from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
# Build the mode solver.
freq0 = tidy3d.C_0 / 1.55
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=[freq0],
)
# Run the server-side mode solver.
mode_data = run_mode_solver(mode_solver)If you prefer, you can run the local version of mode solver through the code mode_data=mode_solver.solve(). This means that the solver will run on your own computer and will not require any credits. However, it's important to note that the local version will not include the group index calculation or subpixel smoothing, even if these options are specified in the simulation. As a result, the local version's results will not perfectly match the server-side ones.
How are the output modes sorted?
num_modes modes closest to the given target_neff. If filter_pol==None, they are simply sorted in order of decreasing effective index. If a polarization filter is selected, the modes are rearranged such that the first n_pol modes in the list are the ones with the selected polarization fraction larger than or equal to 0.5, while the next num_modes - n_pol modes are the ones where it is smaller than 0.5 (i.e. the opposite polarization fraction is larger than 0.5). Within each polarization subset, the modes are still ordered by decreasing effective index. In the example below, the TE modes are returned first in the mode list.import numpy as np
from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
# Define the waveguide.
waveguide = tidy3d.Structure(
geometry=tidy3d.Box(size=(tidy3d.inf, 0.5, 0.22)),
medium=tidy3d.Medium(permittivity=3.47**2),
)
# Build a simulation object including the waveguide.
sim = tidy3d.Simulation(
size=(10, 2.5, 1.5),
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
run_time=1e-12,
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML()),
)
# Plane where we want to solve the modes.
plane = tidy3d.Box(center=(0, 0, 0), size=(0, 2.5, 1.5))
# Mode specification.
mode_spec = tidy3d.ModeSpec(
num_modes=4,
target_neff=3.47,
filter_pol='te',
)
# Build the mode solver.
freq0 = tidy3d.C_0 / 1.55
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=[freq0],
)
# Run the server-side mode solver.
mode_data = run_mode_solver(mode_solver)
# Get the mode polarization fraction.
print("TE polarization fraction:")
print(np.asarray(mode_data.pol_fraction['te']).squeeze())How do I set the mode polarization?
num_modes modes closest to the given target_neff. If filter_pol==None, they are simply sorted in order of decreasing effective index. If a polarization filter is selected, the modes are rearranged such that the first n_pol modes in the list are the ones with the selected polarization fraction larger than or equal to 0.5, while the next num_modes - n_pol modes are the ones where it is smaller than 0.5 (i.e. the opposite polarization fraction is larger than 0.5). The modes are still ordered within each polarization subset by decreasing the effective index.import numpy as np
from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
# Define the waveguide.
waveguide = tidy3d.Structure(
geometry=tidy3d.Box(size=(tidy3d.inf, 0.5, 0.22)),
medium=tidy3d.Medium(permittivity=3.47**2),
)
# Build a simulation object including the waveguide.
sim = tidy3d.Simulation(
size=(10, 2.5, 1.5),
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
run_time=1e-12,
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML()),
)
# Plane where we want to solve the modes.
plane = tidy3d.Box(center=(0, 0, 0), size=(0, 2.5, 1.5))
# Mode specification.
mode_spec = tidy3d.ModeSpec(
num_modes=4,
target_neff=3.47,
filter_pol='te',
)
# Build the mode solver.
freq0 = tidy3d.C_0 / 1.55
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=[freq0],
)
# Run the server-side mode solver.
mode_data = run_mode_solver(mode_solver)
# Get the mode polarization fraction.
print("TE polarization fraction:")
print(np.asarray(mode_data.pol_fraction['te']).squeeze())How do I run the mode solver locally?
.solve() method. For example:from tidy3d.plugins.mode import ModeSolver
# Build the mode solver.
freq0 = tidy3d.C_0 / 1.55
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=[freq0],
)
# Run the local mode solver.
mode_data = mode_solver.solve()How do I run the server-side mode solver?
from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
# Build the mode solver.
freq0 = tidy3d.C_0 / 1.55
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=[freq0],
)
# Run the server-side mode solver.
mode_data = run_mode_solver(mode_solver)To build the mode solver you need to create a simulation object and a plane where you want to calculate the modes, as well as specify the mode characteristics and frequencies of interest. The results are returned in a ModeSolverData object. For more details on how to set up, run, and visualize the solver results, please refer to this notebook.
What are the differences between running the server-side and the local mode solver?
from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
# Build the mode solver.
freq0 = tidy3d.C_0 / 1.55
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=[freq0],
)
# Run the server-side mode solver.
mode_data = run_mode_solver(mode_solver)When using the local version, the solver will run on your own computer and will not require any credits. You can run the local mode solver version using:
from tidy3d.plugins.mode import ModeSolver
# Build the mode solver.
freq0 = tidy3d.C_0 / 1.55
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=[freq0],
)
# Run the local mode solver version.
mode_data = mode_solver.solve()In both cases, the results are returned in a ModeSolverData object. For more details on how to set up, run and visualize the solver results, please refer to this notebook.
Which information can I obtain from the mode solver?
to_dataframe(). We have considered a 500 x 220 nm silicon-on-insulator (SOI) waveguide operating at 1.55 $\mu$m.from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
# Define the waveguide.
waveguide = tidy3d.Structure(
geometry=tidy3d.Box(size=(tidy3d.inf, 0.5, 0.22)),
medium=tidy3d.Medium(permittivity=3.47**2),
)
# Build a simulation object including the waveguide.
sim = tidy3d.Simulation(
size=(10, 2.5, 1.5),
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
run_time=1e-12,
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML()),
)
# Plane where we want to solve the modes.
plane = tidy3d.Box(center=(0, 0, 0), size=(0, 2.5, 1.5))
# Mode specification.
mode_spec = tidy3d.ModeSpec(
num_modes=4,
target_neff=3.47,
group_index_step=True,
)
# Build the mode solver.
freq0 = tidy3d.C_0 / 1.55
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=[freq0],
)
# Run the server-side mode solver.
mode_data = run_mode_solver(mode_solver)
# Print out the results.
mode_data.to_dataframe()For more details on how to set up, run, and visualize the solver results, please refer to this notebook.
How can I get the mode solver information?
from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
# Define the waveguide.
waveguide = tidy3d.Structure(
geometry=tidy3d.Box(size=(tidy3d.inf, 0.5, 0.22)),
medium=tidy3d.Medium(permittivity=3.47**2),
)
# Build a simulation object including the waveguide.
sim = tidy3d.Simulation(
size=(10, 2.5, 1.5),
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
run_time=1e-12,
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML()),
)
# Plane where we want to solve the modes.
plane = tidy3d.Box(center=(0, 0, 0), size=(0, 2.5, 1.5))
# Mode specification.
mode_spec = tidy3d.ModeSpec(
num_modes=4,
target_neff=3.47,
group_index_step=True,
)
# Build the mode solver.
freq0 = tidy3d.C_0 / 1.55
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=[freq0],
)
# Run the server-side mode solver.
mode_data = run_mode_solver(mode_solver)
# Print out the results.
mode_data.to_dataframe()For more details on how to set up, run, and visualize the solver results, please refer to this notebook.
How can I get the mode field distribution?
from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
# Define the waveguide.
waveguide = tidy3d.Structure(
geometry=tidy3d.Box(size=(tidy3d.inf, 0.5, 0.22)),
medium=tidy3d.Medium(permittivity=3.47**2),
)
# Build a simulation object including the waveguide.
sim = tidy3d.Simulation(
size=(10, 2.5, 1.5),
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
run_time=1e-12,
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML()),
)
# Plane where we want to solve the modes.
plane = tidy3d.Box(center=(0, 0, 0), size=(0, 2.5, 1.5))
# Mode specification.
mode_spec = tidy3d.ModeSpec(
num_modes=1,
target_neff=3.47,
group_index_step=True,
)
# Build the mode solver.
freq0 = tidy3d.C_0 / 1.55
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=[freq0],
)
# Run the server-side mode solver.
mode_data = run_mode_solver(mode_solver)
# Get the mode field distribution.
Ey = mode_data.Ey.isel(mode_index=0, f=0)
Ez = mode_data.Ez.isel(mode_index=0, f=0)For more details on how to set up, run, and visualize the solver results, please refer to this notebook.
How can I plot the mode field distribution?
from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
# Define the waveguide.
waveguide = tidy3d.Structure(
geometry=tidy3d.Box(size=(tidy3d.inf, 0.5, 0.22)),
medium=tidy3d.Medium(permittivity=3.47**2),
)
# Build a simulation object including the waveguide.
sim = tidy3d.Simulation(
size=(10, 2.5, 1.5),
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
run_time=1e-12,
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML()),
)
# Plane where we want to solve the modes.
plane = tidy3d.Box(center=(0, 0, 0), size=(0, 2.5, 1.5))
# Mode specification.
mode_spec = tidy3d.ModeSpec(
num_modes=4,
target_neff=3.47,
group_index_step=True,
)
# Build the mode solver.
freq0 = tidy3d.C_0 / 1.55
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=[freq0],
)
# Run the server-side mode solver.
mode_data = run_mode_solver(mode_solver)
# Plot the mode field distribution.
fig, ax = plt.subplots(mode_spec.num_modes, 3, tight_layout=True, figsize=(10, 3*mode_spec.num_modes),
)
for j in range(mode_spec.num_modes):
mode_solver.plot_field("E", "abs", mode_index=j, f=freq0, ax=ax[j, 0])
mode_solver.plot_field("Ey", "real", mode_index=j, f=freq0, ax=ax[j, 1])
mode_solver.plot_field("Ez", "real", mode_index=j, f=freq0, ax=ax[j, 2])
plt.show()For more details on how to set up, run, and visualize the solver results, please refer to this notebook.
How do I plot the mode effective index versus wavelength?
import numpy as np
from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
# Define the waveguide.
waveguide = tidy3d.Structure(
geometry=tidy3d.Box(size=(tidy3d.inf, 0.5, 0.22)),
medium=tidy3d.Medium(permittivity=3.47**2),
)
# Build a simulation object including the waveguide.
sim = tidy3d.Simulation(
size=(10, 2.5, 1.5),
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
run_time=1e-12,
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML()),
)
# Plane where we want to solve the modes.
plane = tidy3d.Box(center=(0, 0, 0), size=(0, 2.5, 1.5))
# Mode specification.
mode_spec = tidy3d.ModeSpec(
num_modes=4,
target_neff=3.47,
group_index_step=True,
)
# Build the mode solver.
wvl = np.linspace(1.5, 1.6, 51)
freqs = tidy3d.C_0 / wvl
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=freqs,
)
# Run the server-side mode solver.
mode_data = run_mode_solver(mode_solver)
# Plot the mode effective index.
n_eff = mode_data.n_eff.values.squeeze()
fig, ax = plt.subplots(1, 1, figsize=(6, 4), tight_layout=True)
for mid in range(mode_spec.num_modes):
ax.plot(wvl, n_eff[:, mid], label=(f"mode {mid}"))For more details on how to set up, run, and visualize the solver results, please refer to this notebook.
How do I plot the mode group index versus wavelength?
import numpy as np
from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
# Define the waveguide.
waveguide = tidy3d.Structure(
geometry=tidy3d.Box(size=(tidy3d.inf, 0.5, 0.22)),
medium=tidy3d.Medium(permittivity=3.47**2),
)
# Build a simulation object including the waveguide.
sim = tidy3d.Simulation(
size=(10, 2.5, 1.5),
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
run_time=1e-12,
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML()),
)
# Plane where we want to solve the modes.
plane = tidy3d.Box(center=(0, 0, 0), size=(0, 2.5, 1.5))
# Mode specification.
mode_spec = tidy3d.ModeSpec(
num_modes=4,
target_neff=3.47,
group_index_step=True,
)
# Build the mode solver.
wvl = np.linspace(1.5, 1.6, 51)
freqs = tidy3d.C_0 / wvl
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=freqs,
)
# Run the server-side mode solver.
mode_data = run_mode_solver(mode_solver)
# Plot the mode group index.
n_group = mode_data.n_group.values.squeeze()
fig, ax = plt.subplots(1, 1, figsize=(6, 4), tight_layout=True)
for mid in range(mode_spec.num_modes):
ax.plot(wvl, n_group[:, mid], label=(f"mode {mid}"))For more details on how to set up, run, and visualize the solver results, please refer to this notebook.
How do I calculate the mode effective area?
import numpy as np
from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
# Define the waveguide.
waveguide = tidy3d.Structure(
geometry=tidy3d.Box(size=(tidy3d.inf, 0.5, 0.22)),
medium=tidy3d.Medium(permittivity=3.47**2),
)
# Build a simulation object including the waveguide.
sim = tidy3d.Simulation(
size=(10, 2.5, 1.5),
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
run_time=1e-12,
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML()),
)
# Plane where we want to solve the modes.
plane = tidy3d.Box(center=(0, 0, 0), size=(0, 2.5, 1.5))
# Mode specification.
mode_spec = tidy3d.ModeSpec(
num_modes=4,
target_neff=3.47,
group_index_step=True,
)
# Build the mode solver.
freq0 = tidy3d.C_0 / 1.55
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=[freq0],
)
# Run the server-side mode solver.
mode_data = run_mode_solver(mode_solver)
# Get the mode effective area.
print("Mode effective area (um^2):")
print(np.asarray(mode_data.mode_area).squeeze())For more details on how to set up, run, and visualize the solver results, please refer to this notebook.
How do I calculate the mode polarization fraction?
import numpy as np
from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
# Define the waveguide.
waveguide = tidy3d.Structure(
geometry=tidy3d.Box(size=(tidy3d.inf, 0.5, 0.22)),
medium=tidy3d.Medium(permittivity=3.47**2),
)
# Build a simulation object including the waveguide.
sim = tidy3d.Simulation(
size=(10, 2.5, 1.5),
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
run_time=1e-12,
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML()),
)
# Plane where we want to solve the modes.
plane = tidy3d.Box(center=(0, 0, 0), size=(0, 2.5, 1.5))
# Mode specification.
mode_spec = tidy3d.ModeSpec(
num_modes=4,
target_neff=3.47,
group_index_step=True,
)
# Build the mode solver.
freq0 = tidy3d.C_0 / 1.55
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=[freq0],
)
# Run the server-side mode solver.
mode_data = run_mode_solver(mode_solver)
# Get the mode polarization fraction.
print("TE polarization fraction:")
print(np.asarray(mode_data.pol_fraction['te']).squeeze())
print("TM polarization fraction:")
print(np.asarray(mode_data.pol_fraction['tm']).squeeze())The TE and TM polarization fractions are defined as the field intensity along the first or the second of the two tangential axes. More precisely, if
E1andE2are the electric field components along the two tangential axes, the TE fraction is defined asintegrate(E1.abs**2) / integrate(E1.abs**2 + E2.abs**2), and theTMfraction is equal to one minus the TE fraction. The tangential axes are defined by popping the normal axis from the list ofx, y, z, so e.g.xandzfor propagation in theydirection.
For more details on how to set up, run and visualize the solver results, please refer to this notebook.
How do I calculate the waveguide mode polarization fraction?
import numpy as np
from tidy3d.plugins.mode import ModeSolver
from tidy3d.plugins.mode.web import run as run_mode_solver
# Define the waveguide.
waveguide = tidy3d.Structure(
geometry=tidy3d.Box(size=(tidy3d.inf, 0.5, 0.22)),
medium=tidy3d.Medium(permittivity=3.47**2),
)
# Build a simulation object including the waveguide.
sim = tidy3d.Simulation(
size=(10, 2.5, 1.5),
grid_spec=tidy3d.GridSpec.auto(min_steps_per_wvl=20, wavelength=1.55),
structures=[waveguide],
run_time=1e-12,
boundary_spec=tidy3d.BoundarySpec.all_sides(boundary=tidy3d.PML()),
)
# Plane where we want to solve the modes.
plane = tidy3d.Box(center=(0, 0, 0), size=(0, 2.5, 1.5))
# Mode specification.
mode_spec = tidy3d.ModeSpec(
num_modes=4,
target_neff=3.47,
group_index_step=True,
)
# Build the mode solver.
freq0 = tidy3d.C_0 / 1.55
mode_solver = ModeSolver(
simulation=sim,
plane=plane,
mode_spec=mode_spec,
freqs=[freq0],
)
# Run the server-side mode solver.
mode_data = run_mode_solver(mode_solver)
# Get the mode waveguide polarization fraction.
print("TE waveguide polarization fraction:")
print(np.asarray(mode_data.pol_fraction_waveguide['te']).squeeze())
print("TM waveguide polarization fraction:")
print(np.asarray(mode_data.pol_fraction_waveguide['tm']).squeeze())The TE and TM polarization fraction using the waveguide definition. If
E1andE2are the electric field components along the two tangential axes andEnis the component along the propagation direction, the TE fraction is defined as1 - integrate(En.abs**2) / integrate(E1.abs**2 + E2.abs**2 + En.abs**2), and theTMfraction is defined as1 - integrate(Hn.abs**2) / integrate(H1.abs**2 + H2.abs**2 + Hn.abs**2), withHdenoting the magnetic field components.
For more details on how to set up, run and visualize the solver results, please refer to this notebook.
Monitors
How do I set a FieldMonitor?
A FieldMonitor object records electromagnetic fields in the frequency domain. You can define a FieldMonitor object by
monitor = FieldMonitor(
center=(1,2,3),
size=(2,2,2),
fields=['Hx'],
freqs=[250e12, 300e12],
name='steady_state_monitor',
colocate=True)For details, please refer to the API reference.
How do I specify apodization?
Apodization applies a windowing function to the Fourier transform of the time-domain fields into frequency-domain ones. It can be used to truncate the beginning and/or end of the time signal, for example, to eliminate the source pulse when studying the eigenmodes of a system. Note that apodization affects the normalization of the frequency-domain fields.
To apply anodization, we first need to define an ApodizationSpec object and then add it to the monitor. For example,
# Apodization to exclude the source pulse from the frequency-domain monitors
apodization = td.ApodizationSpec(start=t_start, width=2e-13)
# Define a FieldMonitor object and add apodization to it
field_mnt = td.FieldMonitor(
center=[0, 0, 0],
size=[4, 2 * np.sqrt(3), 0],
freqs=[freq0],
name="field",
apodization=apodization,
)How do I create field animations?
matplotlib's FuncAnimation to create the animation.phase parameter in the plot_field() function.How do I change the phase of fields obtained from frequency-domain monitors?
apply_phase() function to change the phase of fields obtained from frequency-domain monitors. For example:import numpy as np
# Run the simulation and get the data.
sim_data = tidy3d.web.run(simulation, task_name="task", path="data/data.hdf5", verbose=True)
# Get data from a field monitor.
field_data = sim_data["field_monitor"]
# Change the field phase by phi.
phi = 90 * np.pi / 180
field_phi = field_data.apply_phase(phi)How do I set a FieldTimeMonitor?
A FieldTimeMonitor object records electromagnetic fields in the time domain. You can define a FieldTimeMonitor object by
monitor = FieldTimeMonitor(
center=(1,2,3),
size=(2,2,2),
fields=['Hx'],
start=1e-13,
stop=5e-13,
interval=2,
colocate=True,
name='movie_monitor')For details, please refer to the API reference.
How do I create a time-domain field animation?
Animations are often created from FDTD simulations to provide a more intuitive understanding of the physical phenomena being modeled. These animations can visualize the evolution of the field distribution over time, showing wave propagation, interactions, and other dynamic effects that static images cannot adequately depict.
To create a time-domain field animation, we need to capture the frames at different time instances of the simulation. This can be done by using a FieldTimeMonitor. Usually, an FDTD simulation contains a large number of time steps and grid points. Recording the field at every time step and grid point will result in a large dataset. For the purpose of making animations, this is usually unnecessary. In Tidy3D, we provide both spatial and temporal downsampling options to greatly reduce the animation data size.
Please refer to the detailed tutorial on FDTD animation creation.
How do I plot the time-domain field at a specific time?
Once a simulation with a FieldTimeMonitor is complete, the time-domain field at a specific time instance can be plotted by selecting the specific time instance and using the plot method from the data array. One example is
sim_data['movie_monitor'].Hz.sel(t=1e-13, method='nearest').plot()This line of code plots the z-component of the magnetic field at a time instance closest to 0.1 ps. Most likely, we will need to use the nearest interpolation here since the exact time instance might not be included in the result due to the finite time stepping. However, the difference is usually insignificant, so it is a very good approximation.
How do I set a FluxMonitor?
A FluxMonitor object records power flux in the frequency domain. If the monitor geometry is a 2D box, the total flux through this plane is returned, with a positive sign corresponding to power flow in the positive direction along the axis normal to the plane. If the geometry is a 3D box, the total power coming out of the box is returned by integrating the flux over all box surfaces (except the ones defined in exclude_surfaces). You can define a FluxMonitor object by
monitor = FluxMonitor(
center=(1,2,3),
size=(2,2,0),
freqs=[200e12, 210e12],
name='flux_monitor')For details, please refer to the API reference.
How do I calculate the Poynting vector at a specific surface?
The Poynting vector quantifies the directional energy flux of an electromagnetic field, representing the rate of energy transfer per unit area per unit time and thus characterizing the power flow within the field.
The Poynting vector at a specific plane can be calculated by first placing a FieldMonitor object at that plane to obtain the fields. Then the Poynting vector can be calculated as $\boldsymbol{S} = \boldsymbol{E} \times \boldsymbol{H}$
For example, the z-component of the Poynting vector is calculated from $E_x$, $E_y$,$H_x$, and $H_y$ as $S_z = (E_x H_y^* - E_y H_x^*)$. For time-averaged Poynting vector, we need to multiply by a factor of 0.5.
How do I integrate the Poynting vector at a specific surface?
Since the field data in Tidy3D are natively xarray.DataArray objects, the most convenient way to perform integration is by using the integrate method in xarray. For example, if we want to integrate the Poynting vector on a surface parallel to the xy plane, one needs to compute the z-component of the time-averaged Poynting vector $Sz$ and then
flux = Sz.integrate(coord=["x", "y"])This effectively achieves the same as putting a FluxMonitor object at the same plane and extracting the flux result from the monitor data.
How do I create a flux box?
A flux box can be defined by creating a FluxMonitor object with a 3D geometry. The total power coming out of the box is returned by integrating the flux over all box surfaces (except the ones defined in exclude_surfaces).
For details, please refer to the API reference.
How do I set a FluxTimeMonitor?
A FluxTimeMonitor object records power flux in the time domain. If the monitor geometry is a 2D box, the total flux through this plane is returned, with a positive sign corresponding to power flow in the positive direction along the axis normal to the plane. If the geometry is a 3D box, the total power coming out of the box is returned by integrating the flux over all box surfaces (except the ones defined in exclude_surfaces). You can define a FluxTimeMonitor object by
monitor = FluxTimeMonitor(
center=(1,2,3),
size=(2,2,0),
start=1e-13,
stop=5e-13,
interval=2,
name='flux_vs_time')For details, please refer to the API reference.
How do I set a ModeMonitor?
A ModeMonitor object records complex amplitudes from the modal decomposition of fields on a plane. The amplitudes are defined as mode_solver_data.dot(recorded_field) / mode_solver_data.dot(mode_solver_data), where recorded_field is the field data recorded in the FDTD simulation at the monitor frequencies, and mode_solver_data is the mode data from the mode solver at the monitor plane. This gives the power amplitude of recorded_field carried by each mode. You can define a ModeMonitor object by
mode_spec = ModeSpec(num_modes=3)
monitor = ModeMonitor(
center=(1,2,3),
size=(2,2,0),
freqs=[200e12, 210e12],
mode_spec=mode_spec,
name='mode_monitor')For details, please refer to the API reference.
How do I get the coupling efficiency of a specific waveguide mode?
The coupling efficiency of a specific waveguide mode can be calculated from the mode monitor data by first extracting the complex mode amplitude and then taking the square modulus.
# extract the complex mode amplitude from the mode monitor data
amp = sim_data["mode"].amps.sel(mode_index=0, direction="+")
# compute the coupling efficiency
T = np.abs(amp)**2As an example, you can reference the waveguide Y junction case study.
How do I calculate mode overlap?
Very often we want to calculate the overlap integral of two modes to compute the coupling efficiency. This can be done conveniently using the outer_dot method such as
overlap = waveguide_mode_data_1.outer_dot(waveguide_mode_data_2)where waveguide_mode_data_1 and waveguide_mode_data_2 are ModeSolverData objects from performing the mode solving.
For advanced monitor data manipulation such as integration, please refer to the tutorial.
How do I set a ModeSolverMonitor?
A ModeSolverMonitor object stores the mode field profiles returned by the mode solver in the monitor plane. You can define a ModeSolverMonitor object by
mode_spec = ModeSpec(num_modes=3)
monitor = ModeSolverMonitor(
center=(1,2,3),
size=(2,2,0),
freqs=[200e12, 210e12],
mode_spec=mode_spec,
name='mode_monitor')For details, please refer to the API reference.
How do I set a PermittivityMonitor?
The PermittivityMonitor records the diagonal components of the complex-valued relative permittivity tensor in the frequency domain. You can define a PermittivityMonitor object by
monitor = PermittivityMonitor(
center=(1,2,3),
size=(2,2,2),
freqs=[250e12, 300e12],
name='eps_monitor')For details, please refer to the API reference.
How do I set a FieldProjectionCartesianMonitor?
A FieldProjectionCartesianMonitor object samples electromagnetic near fields in the frequency domain and projects them on a Cartesian observation plane. The center and size fields defines where the monitor will be placed in order to record near fields, typically very close to the structure of interest. The near fields are then projected to far-field locations defined by x, y, and proj_distance, relative to the custom_origin. Here, x and y correspond to a local coordinate system where the local z axis is defined by proj_axis: which is the axis normal to this monitor. If the distance between the near and far field locations is much larger than the size of the device, one can typically set far_field_approx to True, which will make use of the far-field approximation to speed up calculations. If the projection distance is comparable to the size of the device, we recommend setting far_field_approx to False, so that the approximations are not used, and the projection is accurate even just a few wavelengths away from the near field locations. For applications where the monitor is an open surface rather than a box that encloses the device, it is advisable to pick the size of the monitor such that the recorded near fields decay to negligible values near the edges of the monitor. You can define a FieldProjectionCartesianMonitor by
monitor = FieldProjectionCartesianMonitor(
center=(1,2,3),
size=(2,2,2),
freqs=[250e12, 300e12],
name='n2f_monitor',
custom_origin=(1,2,3),
x=[-1, 0, 1],
y=[-2, -1, 0, 1, 2],
proj_axis=2,
proj_distance=5
)For details, please refer to the API reference.
How do I set a FieldProjectionAngleMonitor?
A FieldProjectionAngleMonitor object samples electromagnetic near fields in the frequency domain and projects them at given observation angles. The center and size fields defines where the monitor will be placed in order to record near fields, typically very close to the structure of interest. The near fields are then projected to far-field locations defined by phi, theta, and proj_distance, relative to the custom_origin. If the distance between the near and far field locations is much larger than the size of the device, one can typically set far_field_approx to True, which will make use of the far-field approximation to speed up calculations. If the projection distance is comparable to the size of the device, we recommend setting far_field_approx to False, so that the approximations are not used, and the projection is accurate even just a few wavelengths away from the near field locations. For applications where the monitor is an open surface rather than a box that encloses the device, it is advisable to pick the size of the monitor such that the recorded near fields decay to negligible values near the edges of the monitor. You can define a FieldProjectionAngleMonitor object by
monitor = FieldProjectionAngleMonitor(
center=(1,2,3),
size=(2,2,2),
freqs=[250e12, 300e12],
name='n2f_monitor',
custom_origin=(1,2,3),
phi=[0, np.pi/2],
theta=np.linspace(-np.pi/2, np.pi/2, 100)
)For details, please refer to the API reference.
How do I set a FieldProjectionKSpaceMonitor?
A FieldProjectionKSpaceMonitor object samples electromagnetic near fields in the frequency domain and projects them on an observation plane defined in k-space. The center and size fields defines where the monitor will be placed in order to record near fields, typically very close to the structure of interest. The near fields are then projected to far-field locations defined in k-space by ux, uy, and proj_distance, relative to the custom_origin. Here, ux and uy are associated with a local coordinate system where the local ‘z’ axis is defined by proj_axis: which is the axis normal to this monitor. If the distance between the near and far field locations is much larger than the size of the device, one can typically set far_field_approx to True, which will make use of the far-field approximation to speed up calculations. If the projection distance is comparable to the size of the device, we recommend setting far_field_approx to False, so that the approximations are not used, and the projection is accurate even just a few wavelengths away from the near field locations. For applications where the monitor is an open surface rather than a box that encloses the device, it is advisable to pick the size of the monitor such that the recorded near fields decay to negligible values near the edges of the monitor. You can define a FieldProjectionKSpaceMonitor object by
monitor = FieldProjectionKSpaceMonitor(
center=(1,2,3),
size=(2,2,2),
freqs=[250e12, 300e12],
name='n2f_monitor',
custom_origin=(1,2,3),
proj_axis=2,
ux=[0.1,0.2],
uy=[0.3,0.4,0.5]
)For details, please refer to the API reference.
How do I set a DiffractionMonitor?
A DiffractionMonitor object uses a 2D Fourier transform to compute the diffraction amplitudes and efficiency for allowed diffraction orders. You can define a DiffractionMonitor object by
monitor = DiffractionMonitor(
center=(1,2,3),
size=(inf,inf,0),
freqs=[250e12, 300e12],
name='diffraction_monitor',
normal_dir='+',
)For details, please refer to the API reference.
Data Visualization and Postprocessing
How do I plot an object with a spatial definition?
obj.plot(x=0) will plot the object on the x=0 plane. Note that y and z are alternatively accepted to specify other planar axes. Include the ax argument to plot to an existing axis, ie. obj.plot(y=0, ax=ax).How do I change the object plotting characteristics (facecolor, edgecolor, etc)?
plot(), for example obj.plot(x=0, edgecolor='blue', fill=False). These keyword arguments correspond to those fed to Matplotlib Patches.How do I change the global plot characteristics (title, size, etc)?
Axes, which can be manipulated, for example ax = obj.plot(x=0); ax.set_title('my_title').How do I access the data of a specific monitor?
You can access the data of a specific monitor by its name. For instance, supposing you have a field monitor and set its name to “field”, you can refer to this name after running the simulation to get the monitor’s data.
sim_data = tidy3d.web.run(simulation, task_name="task", path="data/data.hdf5", verbose=True)
field_data = sim_data["field"]
How do I interpolate the electromagnetic field data at the Yee cell centers?
To interpolate the electromagnetic fields to the Yee cell centers, you can use the method at_centers(monitor_name). For example:
# Run the simulation and get the results.
sim_data = tidy3d.web.run(simulation, task_name="task", path="data/data.hdf5", verbose=True)
# Interpolate the field at the Yee cell centers.
field_data_centered = sim_data.at_centers("monitor_name").interp(f=freq0)
By default, the electromagnetic fields are colocated to Yee grid boundaries. If you want to colocate data into custom coordinates, set
colocate=Falsein field monitors to use the raw data on the Yee grid and avoid double interpolation.
For more details on visualizing and postprocessing simulation data, see this notebook.
How do I get the monitor's data from a SimulationData object?
To get the data of a particular monitor, you can use its name. For example, if you have a field monitor and have given it the name “field”, you can refer to this name to retrieve the monitor’s data after the simulation is run.
sim_data = tidy3d.web.run(simulation, task_name="task", path="data/data.hdf5", verbose=True)
field_data = sim_data["field"]
How do I select the data at a certain coordinate value (i.e. x=0.0, f=200e12)?
The simulation data is stored as a DataArray object using the xarray package. You can think of it as a dataset where data is stored as a large multi-dimensional array (like a numpy array) and the coordinates along each of the dimensions are specified, so it is easy to work with.
You can use the sel() method to select data at certain coordinates. For example:
# Run the simulation and get the data.
sim_data = tidy3d.web.run(simulation, task_name="task", path="data/data.hdf5", verbose=True)
# Get all the data from a field monitor.
field_data = sim_data["field"]
# Get field data for a specific frequency.
field_freq = field_data.sel(f=200e14)
# Get field data for a specific position and frequency.
field_pos_freq = field_data.sel(z=0, f=200e14)You can find detailed information about simulation data visualization and postprocessing in this tutorial.
How do I get the monitor data at a certain index?
The simulation data is stored as a DataArray object using the xarray package. You can think of it as a dataset where data is stored as a large multi-dimensional array (like a numpy array) and the coordinates along each of the dimensions are specified, so it is easy to work with.
You can use the isel() method to select data at a certain coordinate index. For example:
# Run the simulation and get the data.
sim_data = tidy3d.web.run(simulation, task_name="task", path="data/data.hdf5", verbose=True)
# Get all the data from a field monitor.
field_data = sim_data["field"]
# Get field data for a specific frequency index.
field_freq_3 = field_data.isel(f=3)You can find detailed information about simulation data visualization and postprocessing in this tutorial.
How do I interpolate the monitor data at various coordinate values?
The simulation data is stored as a DataArray object using the xarray package. You can think of it as a dataset where data is stored as a large multi-dimensional array (like a numpy array) and the coordinates along each of the dimensions are specified, so it is easy to work with.
You can use the interp() method to interpolate data at certain coordinates. For example:
# Run the simulation and get the data.
sim_data = tidy3d.web.run(simulation, task_name="task", path="data/data.hdf5", verbose=True)
# Get all the data from a field monitor.
field_data = sim_data["field"]
# Interpolate field data at a specific frequency.
field_freq = field_data.interp(f=200e14)
# Interpolate field data at a specific position.
field_pos = field_data..interp(x=0, y=0, z=0)You can find detailed information about simulation data visualization and postprocessing in this tutorial.
How do I get the real part, imaginary part, or absolute value of complex-valued simulation data?
The simulation data is stored as a DataArray object using the xarray package. You can think of it as a dataset where data is stored as a large multi-dimensional array (like a numpy array) and the coordinates along each of the dimensions are specified, so it is easy to work with.
Some of the available convenience methods provided by DataArray can be used to obtain the real, imaginary, or absolute value of complex-valued simulation data. For instance:
# Run the simulation and get the data.
sim_data = tidy3d.web.run(simulation, task_name="task", path="data/data.hdf5", verbose=True)
# Get all the data from a field monitor.
field_data = sim_data["field"]
# Get the real part of Ex field component.
ex_real = field_data.Ex.real
# Get the imaginary part of Ey field component.
ey_imag = field_data.Ey.imag
# Get the absolute value of Ez field component.
ez_abs = abs(field_data.Ez)
You can find detailed information about simulation data visualization and postprocessing in this tutorial.
How do I get the raw monitor data values as a numpy array?
The simulation data is stored as a DataArray object using the xarray package. You can think of it as a dataset where data is stored as a large multi-dimensional array (like a numpy array) and the coordinates along each of the dimensions are specified, so it is easy to work with.
The example below shows how to get the raw monitor data as numpy arrays.
# Run the simulation and get the data.
sim_data = tidy3d.web.run(simulation, task_name="task", path="data/data.hdf5", verbose=True)
# Get all the data from a flux monitor.
flux_data = sim_data["flux_monitor"]
# Get the flux values as numpy arrays.
print(f"Shape of flux dataset = {flux_data.shape}\n.")
print(f"Frequencies in dataset = {flux_data.coords.values} \n.")
print(f"Flux values in dataset = {flux_data.values}\n.")You can find detailed information about simulation data visualization and postprocessing in this tutorial.
How do I get a specific field component from a FieldMonitor or FieldTimeMonitor?
Some of the available convenience methods provided by the DataArray can be used to get a specific field component from a FieldMonitor or FieldTimeMonitor. For instance:
# Run the simulation and get the data.
sim_data = tidy3d.web.run(simulation, task_name="task", path="data/data.hdf5", verbose=True)
# Get all the data from a field monitor.
field_data = sim_data["field"]
# Get the Ex field component.
ex = field_data.Ex
# Get the Hy field component.
hy = field_data.Hy
You can find detailed information about simulation data visualization and postprocessing in this tutorial.
How do I plot the monitor data as a function of one of its coordinates?
To plot the monitor data as a function of one of its coordinates, you can use mon_data.plot() if the data is already 1D. For example:
# Run the simulation and get the data.
sim_data = tidy3d.web.run(simulation, task_name="task", path="data/data.hdf5", verbose=True)
# Get data from a flux monitor.
flux_data = sim_data["flux_monitor"].flux
# Plot the flux data.
f, (ax1, ax2) = plt.subplots(1, 2, tight_layout=True, figsize=(8, 3))
flux_data.plot(ax=ax1)
ax2.plot(flux_data.f, flux_data.values)
plt.show()To select the x axis data explicitly or plot all the data on same plot, use mon_data.plot.line(x='f', ax=ax). Note that for all the plottings, if ax is not supplied, it will be created.
You can find detailed information about simulation data visualization and postprocessing in this tutorial.
How do I plot the simulation structure on top of my field plot?
You can use the plot_field() function to plot the structure on top of the simulated fields. For example:
# Run the simulation and get the data.
sim_data = tidy3d.web.run(simulation, task_name="task", path="data/data.hdf5", verbose=True)
# Plot the Ex field data and the structure.
ax = sim_data.plot_field(
field_monitor_name="field",
field_name="Ex",
val='real',
eps_alpha=0.2,
phase=0,
)You can find detailed information about simulation data visualization and postprocessing in this tutorial.
How do I project electromagnetic near-field data to the far field?
In Tidy3D you can use field projections to obtain electromagnetic field data far away from a structure with knowledge of only near-field data. When projecting fields, geometric approximations can be invoked to allow computing fields far away from the structure quickly and with good accuracy, but in Tidy3D we can also turn these approximations off when projecting fields at intermediate distances away, which gives a lot of flexibility. These field projections are particularly useful for eliminating the need to simulate large regions of empty space around a structure.
See this tutorial for details on:
- How to compute projected fields on your local machine after a simulation is run, or on our servers during the simulation run.
- How to extract various quantities related to projected fields such as fields in different coordinate systems, power, and radar cross section.
- How, when far field approximations are used, the fields can dynamically be re-projected to new distances without having to run a new simulation.
- When geometric far field approximations should and should not be invoked, depending on the projection distance and the geometry of the structure.
- How to set up projections for finite-sized objects (e.g., scattering at a sphere) vs. thin but large-area structures (e.g., metasurfaces).
Scattering Matrix
How do I compute scattering matrix parameters for modeling my device?
To compute scattering matrix parameters, you need to create a base tidy3d.Simulation (without the modal sources or monitors used to compute S-parameters) and include tidy3d.plugins.smatrix.Port objects. These ports will be converted into modal sources and monitors later, so they require a mode specification and a definition of the direction that points into the system. You should also give them names to refer to later. For example:
from tidy3d.plugins.smatrix.smatrix import Port
num_modes = 1
# Port definition.
port_right_top = Port(
center=[-5, 3, 0],
size=[0, 4, 2],
mode_spec=tidy3d.ModeSpec(num_modes=num_modes),
direction="-",
name="right_top",
)Next, add the base simulation and ports to the tidy3d.plugins.smatrix.ComponentModeler, along with the frequency of interest and a name for saving the batch of simulations that will get created later.
from tidy3d.plugins.smatrix.smatrix import ComponentModeler
modeler = ComponentModeler(
simulation=sim,
ports=ports,
freqs=[freq0],
verbose=True
)
modeler.plot_sim(z=0)With the component modeler defined, you should call it’s .solve() method to run a batch of simulations to compute the S matrix. The tool will loop through each port and create one simulation per mode index (as defined by the mode specifications), where a unique modal source is injected. Each of the ports will also be converted to mode monitors to measure the mode amplitudes and normalization.
from tidy3d.plugins.smatrix.smatrix import Port
smatrix = modeler.run(path_dir="data")The scattering matrix returned by the solve is an xr.DataArray relating the port names and mode indices. For example smatrix.loc[dict(port_in=name1, mode_index_in=mode_index1, port_out=name2, mode_index_out=mode_index_2)] gives the complex scattering matrix element.
See this tutorial for more details on computing the scattering matrix.
How do I specify a Port in the scattering matrix calculation?
To compute scattering matrix parameters, you need to create a base tidy3d.Simulation (without the modal sources or monitors used to compute S-parameters) and include tidy3d.plugins.smatrix.Port objects. These ports will be converted into modal sources and monitors later, so they require both some mode specification and a definition of the direction that points into the system. You should also give them names to refer to later. For example:
from tidy3d.plugins.smatrix.smatrix import Port
num_modes = 1
# Port definition.
port_right_top = Port(
center=[-5, 3, 0],
size=[0, 4, 2],
mode_spec=tidy3d.ModeSpec(num_modes=num_modes),
direction="-",
name="right_top",
)How do I specify mappings between scattering matrix elements?
You can specify mappings between scattering matrix elements that you want to be equal up to a multiplicative factor. You can define these as element_mappings in the tidy3d.plugins.smatrix.ComponentModeler.
“Indices” are defined as a tuple of (port_name: str, mode_index: int)
“Elements” are defined as a tuple of output and input indices, respectively.
The element mappings are therefore defined as a tuple of (element, element, value) where the first element is set by the value of the 2nd element times the supplied value.
See this tutorial for more details on computing the scattering matrix.
Resonance Finder
How do I set the ResonanceFinder?
The tidy3d.plugins.resonance.ResonanceFinder plugin allows one to find resonances and extract their information from time domain field monitors without the necessity of waiting for the fields to decay completely. The ResonanceFinder plugin needs tidy3d.FieldTimeMonitor to record the field as a function of time. Importantly, you should start the monitors after the source pulse has decayed.
After setting up and running the simulation, you should construct a ResonanceFinder object and then call run() on the list of FieldTimeData objects. This will add up the signals from all field time monitors included in the simulation before searching for resonances.
from tidy3d.plugins.resonance import ResonanceFinder
resonance_finder = ResonanceFinder(freq_window=(190e14, 210e14))
resonance_data = resonance_finder.run(signals=sim_data.data)
resonance_data.to_dataframe()The run() method returns an xr.Dataset containing the decay rate, Q factor, amplitude, phase, and estimation error for each resonance as a function of frequency.
See this tutorial for more details on the ResonanceFinder plugin.
How do I get resonance quality factors?
To calculate low-quality factor resonances using Tidy3D, you can build and run a simulation until the electromagnetic fields fully decay to negligible values within the simulation domain. Then, you can obtain the resonance quality factor from the spectral response obtained from frequency-domain monitors.
However, when looking for long-lived resonances, the total time to the fields fully decay within the simulation domain can be extremely long. In this situation, the tidy3d.plugins.resonance.ResonanceFinder plugin allows one to find resonances and extract their information from time domain field monitors without the necessity of waiting for the fields to decay completely. The ResonanceFinder plugin needs tidy3d.FieldTimeMonitor to record the field as a function of time.
See this tutorial for more details on the ResonanceFinder plugin.
How do I calculate photonic band diagrams using the ResonanceFinder?
To calculate photonic band diagrams using Tidy3D you can excite the structure with several tidy3d.PointDipole sources and measure the response with several tidy3d.FieldTimeMonitor monitors. You should excite modes with a fixed Bloch wavevector by using tidy3d.BlochBoundary boundary conditions. Then, use the tidy3d.plugins.resonance.ResonanceFinder to find the resonant frequencies. By sweeping the Bloch wavevector, you can obtain the complete band structure of a photonic crystal structure.
This notebook shows a complete example of calculating a band diagram of a photonic crystal slab.
How do I calculate the effective mode volume?
To calculate the effective mode volume, you should include a tidy3d.FieldMonitor to record the electromagnetic fields within a box enclosing the cavity resonance. After running the simulation, you can follow this example to obtain the effective mode volume.
How to Ensure the Calculated Quality Factor is Accurate?
To calculate low-quality factor resonances using Tidy3D you can build and run a simulation until the electromagnetic fields fully decay to negligible values within the simulation domain. Then, you can obtain the resonance quality factor from the spectral response obtained from frequency-domain monitors. In this case, it is crucial to ensure the fields have fully decayed by the end of the simulation to get an accurate spectral response.
When looking for long-lived resonances, the total time to the fields fully decay within the simulation domain can be extremely long. In this situation, the tidy3d.plugins.resonance.ResonanceFinder plugin allows one to find resonances and extract information from time domain field monitors without the necessity of waiting for the fields to decay completely. To calculate accurate quality factors using the ResonanceFinder you should start the monitors after the source pulse has decayed.
In any case, a grid resolution convergence test is also essential to improve the results.
See this tutorial for more details on the ResonanceFinder plugin.
How do I calculate the Purcell factor?
You can calculate the Purcell factor from the cavity quality factor and effective mode volume using tidy3d.FieldMonitor and the tidy3d.plugins.resonance.ResonanceFinder plugin, as detailed in this tutorial.
Alternatively, you can calculate the Purcell factor as the ratio between the dipole power emitted in the final device and in the bulk semiconductor using tidy3d.FluxMonitor. Refer to this example for more details on this later approach.
Inverse Design
What is adjoint simulation?
adjoint plugin allows users to take derivatives of arbitrary functions involving Tidy3D simulations through the use of the "adjoint method". The advantage of the adjoint method is that the gradients can be computed using only two FDTD simulations, the forward and the adjoint one, independent of the number of parameters. This makes it possible to do gradient-based optimization or sensitivity analysis of devices with enormous numbers of parameters with minimal computational overhead. How many simulations are performed in adjoint calculations?
forward and the adjoint one, are performed when running inverse design optimizations using the adjoint plugin. How is the adjoint simulation billed?
forward and the adjoint simulations are billed when running inverse design optimizations using the adjoint plugin. That represents a significant reduction in computation cost as the adjoint method allows one to calculate the gradient of an objective function with respect to thousands of design parameters in only two simulations.How to install jax?
How do I set an inverse design problem?
To create an adjoint inverse design setup, you need to use a special Simulation subclass called tidy3d.plugins.adjoint.JaxSimulation, which is a jax-compatible stand in for Simulation and behaves almost entirely the same, except for a few important differences:
- This feature allows for the inclusion of an extra field (
.input_structures) consisting ofjax-compatible Tidy3D structures. For example, the tidy3d.plugins.adjoint.JaxStructure, which contains a.mediumand a.geometryfield, both of which may depend on the design parameters. The final gradients of the objective function will be given with respect to the values of the fields mentioned above. - It accepts the additional field
.output_monitors, that defines the set of monitors and corresponding data that the objective function will depend on.
jax.value_and_grad to both compute the objective function and the gradient with respect to the design parameters. The objective function gradients can then feed a gradient-based optimization algorithm to drive the inverse design process. What are the differences between adjoint shape, topology, and level set optimizations?
adjoint plugin allows users to take derivatives of arbitrary functions involving Tidy3D simulations through the use of the "adjoint method". The advantage of the adjoint method is that the gradients can be computed using only two FDTD simulations, the forward and the adjoint one, independent of the number of parameters. This makes it possible to do gradient-based optimization or sensitivity analysis of devices with enormous numbers of parameters with minimal computational overhead.How do I set an adjoint shape optimization?
To create an adjoint shape optimization setup, you need to provide jax-compatible geometries such as tidy3d.plugins.adjoint.JaxBox or tidy3d.plugins.adjoint.JaxPolySlab when creating objects of type tidy3d.plugins.adjoint.JaxStructure. The structures should then be included in the .input_structures parameter of the tidy3d.plugins.adjoint.JaxSimulation object. In addition, you must specify an adjoint compatible monitor in .output_monitors, which defines the set of monitors and corresponding data that the objective function will depend on.
jax.value_and_grad to both compute the objective function and the gradient with respect to the design parameters. The objective function gradients can then feed a gradient-based optimization algorithm to drive the inverse design process. How do I set an adjoint topology optimization?
To create an adjoint topology (or density-based) optimization setup, you can control the permittivity values of a tidy3d.plugins.adjoint.JaxCustomMedium based on the optimization design parameters. After that, you need to include it in a tidy3d.plugins.adjoint.JaxStructure. Be sure of adding the adjoint structures in the .input_structures parameter of the tidy3d.plugins.adjoint.JaxSimulation object. In addition, you must specify an adjoint compatible monitor in .output_monitors, which defines the set of monitors and corresponding data that the objective function will depend on.
jax.value_and_grad to both compute the objective function and the gradient with respect to the design parameters. The objective function gradients can then feed a gradient-based optimization algorithm to drive the inverse design process. How do I create an adjoint parameterized level set optimization?
To create an adjoint parameterized level set-based optimization setup, you should use the design parameters as the control knots of a level set surface. Then, create a tidy3d.plugins.adjoint.JaxCustomMedium and set the permittivity values based on the zero level isocontour obtained from the level set surface. After that, you need to include it in a tidy3d.plugins.adjoint.JaxStructure. Be sure of adding the adjoint structures in the .input_structures parameter of the tidy3d.plugins.adjoint.JaxSimulation object. In addition, you must specify an adjoint compatible monitor in .output_monitors, that defines the set of monitors and corresponding data that the objective function will depend on.
jax.value_and_grad to both compute the objective function and the gradient with respect to the design parameters. The objective function gradients can then feed a gradient-based optimization algorithm to drive the inverse design process. How do I include fabrication constraints in adjoint shape optimization?
To ensure reliable fabrication of a device, it is crucial to avoid using feature sizes below a certain radius of curvature when performing inverse design. To achieve this, you can use a penalty function that estimates the radius of curvature around each boundary vertex and applies a substantial penalty to the objective function if the value falls below the minimum radius. The code example below demonstrates how to use the tidy3d.plugins.adjoint.utils.penalty.RadiusPenalty function.
from tidy3d.plugins.adjoint.utils.penalty import RadiusPenalty
penalty = RadiusPenalty(min_radius=.150, alpha=1.0, kappa=10.0)
vertices0 = jnp.array(make_taper(ys0).vertices)
penalty_value = penalty.evaluate(vertices0)
How do I include fabrication constraints in adjoint topology optimization?
To ensure reliable fabrication of a device, it is crucial to avoid using feature sizes below a certain radius of curvature when performing inverse design. To achieve this in topology (density-based) optimization, you can use a conic density filter, which is popular in topology optimization problems, to enforce a minimum feature size specified by the filter_radius variable. Next, a hyperbolic tangent projection function can be applied to eliminate grayscale and obtain a binarized permittivity pattern. The code example below demonstrates how to apply the conic filter and the projection function to the design parameters before obtaining the permittivity values.
from tidy3d.plugins.adjoint.utils.filter import ConicFilter, BinaryProjector
conic_filter = ConicFilter(radius=filter_radius, design_region_dl=dr_grid_size)
def tanh_projection(x, beta, eta=0.5):
tanhbn = jnp.tanh(beta * eta)
num = tanhbn + jnp.tanh(beta * (x - eta))
den = tanhbn + jnp.tanh(beta * (1 - eta))
return num / den
def filter_project(x, beta, eta=0.5):
x = conic_filter.evaluate(x)
return tanh_projection(x, beta=beta, eta=eta)
def get_eps_values(params, beta):
params = filter_project(params, beta=beta)
eps_values = eps_min + (eps_max - eps_min) * params
return eps_values
How do I include fabrication constraints in adjoint level set optimization?
To ensure reliable fabrication of a device, it is crucial to avoid using feature sizes below a certain feature size when performing inverse design. To achieve this in level set optimization, you can use penalty functions to apply a substantial penalty to the objective function if the curvature and gap size values fall below a minimum feature size. This example shows how to calculate the minimum radius of curvature and the minimum gap size penalty functions using the level set surface as input.
How do I export the final inverse design structure to GDS?
After performing adjoint inverse designs using the adjoint plugin, you can export the final structure to GDS files using the function .to_gds_file().
from tidy3d.plugins.adjoint.utils.penalty import RadiusPenalty
# Convert the final adjoint simulation to a regular one.
sim_final = sim_adj.to_simulation()[0]
# Export the final simulation to GDS.
sim_final.to_gds_file(fname="inverse_design.gds", z=0, permittivity_threshold=6, frequency=200e14)














