The FDTD Method Demystified
By Weiliang JinThe finite-difference time-domain (FDTD) method is a powerful full-wave simulation tool for solving Maxwell’s equations. It is widely used in modeling the behavior of light in nanophotonic devices. In this section, we introduce the fundamental concepts behind FDTD and how to use it to simulate a wide range of phenomena in photonics. As an example, we show how to compute the scattering cross-section of a dielectric sphere and benchmark it against Mie Theory.
Session 1: The FDTD Method Demystified¶
Mie scattering describes the interaction of electromagnetic waves, such as light, with small particles whose dimensions are comparable to the wavelength of the incident light. This theory, named after German physicist Gustav Mie, provides an exact solution to Maxwell's equations for the scattering of electromagnetic waves by spherical particles.
From Mie theory, we can calculate the scattering cross section of single homogeneous (or core/shell) spheres ($C_{sca}$) as
$$ C_{sca} = \frac{2\pi}{k^{2}}\sum_{n}\left(2n+1\right)\left(|a_{n}|^{2} + |b_{n}|^{2}\right), $$where $k$ is the wave number, $a_{n}$ and $b_{n}$ are the electric and magnetic Mie coefficients, and $n$ is the order of the multipole moments [1]. The scattering cross section relates the incident irradiance ($I_{i}$) and the energy scattering rate ($W_{sca}$) by $S_{sca} = W_{sca}/I_{i}$.
The ratio between $C_{sca}$ and the particle cross-sectional area projected onto a plane perpendicular to the incident beam ($G$) results in the scattering efficiency [1]:
$$ Q_{sca} = \frac{C_{sca}}{G}. $$In the following activities, you will calculate the scattering efficiency of sphere nanoparticles using the FDTD method and an analytical solution provided by the PyMieScatt package.
Example¶
In this example, we will walk you through the process of setting up and running an FDTD simulation to calculate the scattering efficiency of a dielectric nanosphere. Then, you will compare the simulation and the analytical results. Consider a single Si spherical nanoparticle with a diameter of 0.15 $\mu m$ and a refractive index value of 3.48 under plane wave excitation and light wavelength ranging from 0.45 $\mu m$ to 0.75 $\mu m$. Use 150 frequency points to sample the optical response.
You can develop this example using the Tidy3D Python notebook or the Graphical User Interface (GUI) web-based environments.
Step 1 - Import Necessary Libraries¶
If you use the Python notebook interface, start by including the necessary libraries below. Otherwise, create a new project at the GUI following the FDTD Walkthrough tutorial.
Use
pip install pymiescattto install thePyMieScattpackage.
import numpy as np
import matplotlib.pyplot as plt
import tidy3d as td
print(td.__version__)
import tidy3d.web as web
import PyMieScatt as pms
2.5.0
Step 2 - Simulation Setup¶
Python: define the structure and simulation parameters, as below:
n_mat = 3.48 # index of refraction of the sphere
permittivity = n_mat **2 # Permittivity of the sphere
sphere_d = 0.15 # Diameter of the sphere in um
lam_beg = 0.45 # Minimum wavelength in um
lam_end = 0.75 # Maximum wavelength in um
Nlambda = 150 # Number of wavelength points to sample the optical response.
lambdas = np.linspace(lam_beg, lam_end, Nlambda)
resolution = 30 # Grid resolution per shortest wavelength in the medium.
# In this simulation, the shortest wavelength of interest in vacuum is `lam_beg`, which
# is further reduced to `lam_beg/3.48` inside the sphere made of high-index material.
run_time = 1e-13 # Simulation run time in s
spacing = (lam_end + lam_beg) / 2 # Spacing between the sphere to the simulation domain boundaries
sim_size = [sphere_d + 2 * spacing] * 3 # Simulation domain size
GUI: you can define the simulation parameters as variables in the Parameter tab.
Step 3 - Medium Definition¶
Python: define the sphere medium using the
Mediumobject.
sphere_mat = td.Medium(permittivity=permittivity) # Define the sphere material
GUI: switch to the Parameter tab, and define the medium there. See the Medium tutorial for more information.
Step 4 - Sphere Structure¶
Python: use the medium and the sphere diameter to set up a
Structureobject.
# Define a sphere
sphere = td.Structure(
geometry=td.Sphere(radius=sphere_d / 2),
medium=sphere_mat,
)
GUI: click the Add Structure command to set up the sphere. See the Structure tutorial for more information.
freq0 = td.C_0 / (lam_beg + lam_end) * 2 # Central frequency in Hz
fwidth = (td.C_0 / lam_beg - td.C_0 / lam_end) / 2 # Source frequency width in Hz
freqs = td.C_0 / lambdas
source_time = td.GaussianPulse(freq0=freq0, fwidth=fwidth) # Source time profile
# Define a TFSF source
source = td.TFSF(
center=(0, 0, 0),
size=[
sphere_d + 0.5 * spacing,
]
* 3,
source_time=source_time,
injection_axis=2, # Inject along the z axis
direction="+", # In the positive direction, i.e. along z+
)
GUI: click Add Source command, select the TFSF source type, and set its parameters, size, and position. See the Sources tutorial for more information.
Step 6 - Define Monitors¶
To compute the scattering cross section, create two FluxMonitor boxes to measure the scattered and the incident powers. Name the first one flux_out and set its dimensions to sphere_d + spacing. Name the latter flux_inj and set its dimensions to the simulation domain size.
Python: define FluxMonitors to measure the scattered and the incident powers.
# Define a monitor to measure scattered power
flux_out = td.FluxMonitor(
center=source.center,
size=[
sphere_d + spacing,
]
* 3,
freqs=freqs,
name="flux_out",
)
# Define a monitor to measure incident power in a reference simulation
flux_inj = td.FluxMonitor(
center=source.center,
size=[td.inf, td.inf, 0],
freqs=freqs,
name=f"flux_inj",
)
GUI: to create the
FluxMonitors, click Add Monitor command, select the FluxMonitor type, and set its name, parameters, size, and position. See the Monitors tutorial for more information.
Step 7 - Simulation Object¶
Now, you will put together the previously defined structure, source, and monitors into Tidy3D Simulation objects. You should define a real simulation with the sphere and a normalization simulation without the sphere.
Python: In the example below, you must provide all the
sim_size,structures,sources, andmonitorsdefined previously. Note that you need to assign theflux_outmonitor in the real simulation and theflux_injmonitor to the reference simulation. To create the reference simulation, you can use theupdated_copy()method assigning an empty list tostructuresandflux_injtomonitors.
# Define the real simulation
sim = td.Simulation(
size=sim_size,
grid_spec=td.GridSpec.uniform(dl=lam_beg / n_mat / resolution),
structures=[sphere],
sources=[source],
monitors=[flux_out],
run_time=run_time,
boundary_spec=td.BoundarySpec.all_sides(td.PML()),
)
# Define the reference simulation
empty_sim = sim.updated_copy(structures=[], monitors=[flux_inj])
GUI: Go through the CONFIGURATION section to set up the simulation parameters. You can see the FDTD Walkthrough tutorial to set up the simulation domain and find detailed examples on Grid Specification, Run Time and Shutoff, and Boundary Conditions. In the real simulation, disable the
flux_injmonitor. Once you conclude the setup of the real simulation, click "Save As" to make a simulation copy. Open this copy and disable (1) the sphere structure and (2) theflux_outmonitor.
print(f"Number of grid cells: {sim.num_cells: 1.2e}; time steps {sim.tmesh.size: 1.2e}")
Number of grid cells: 3.86e+07; time steps 1.22e+04
Step 8 - Run Simulations¶
Check the simulation setup to verify if all the components are in their correct places and run the simulations.
Python: Use
sim.plot_3d()to visualize the simulation setup. Then, define a simulation batch and run two simulations in parallel.
sim.plot_3d() # Visualize the simulation in 3D
# Define a simulation batch including the real and the reference simulations.
sims = {"real": sim, "reference": empty_sim}
# Run the batch.
batch = web.Batch(simulations=sims)
batch_results = batch.run(path_dir="data")
21:06:16 -03 Created task 'real' with task_id 'fdve-0083fda1-0d36-4690-b59d-a55674ff59f2' and task_type 'FDTD'.
View task using web UI at 'https://tidy3d.simulation.cloud/workbench?taskId=fdve-0083fda1-0d3 6-4690-b59d-a55674ff59f2'.
21:06:18 -03 Created task 'reference' with task_id 'fdve-4c6c7e28-6b2e-492f-88d3-9866b4aedad7' and task_type 'FDTD'.
View task using web UI at 'https://tidy3d.simulation.cloud/workbench?taskId=fdve-4c6c7e28-6b2 e-492f-88d3-9866b4aedad7'.
21:06:28 -03 Started working on Batch.
21:06:30 -03 Maximum FlexCredit cost: 0.295 for the whole batch.
Use 'Batch.real_cost()' to get the billed FlexCredit cost after the Batch has completed.
21:07:04 -03 Batch complete.
GUI: After verifying the simulation setup in the 3D Chart, click the Run button to start the simulation.
print(batch_results["real"].log)
21:07:39 -03 loading simulation from data/fdve-0083fda1-0d36-4690-b59d-a55674ff59f2.hdf5
Simulation domain Nx, Ny, Nz: [338, 338, 338] Applied symmetries: (0, 0, 0) Number of computational grid points: 3.9304e+07. Using subpixel averaging: True Number of time steps: 1.2201e+04 Automatic shutoff factor: 1.00e-05 Time step (s): 8.1971e-18 Compute source modes time (s): 0.3394 Compute monitor modes time (s): 0.0003 Rest of setup time (s): 2.6448 Running solver for 12201 time steps... - Time step 488 / time 4.00e-15s ( 4 % done), field decay: 1.00e+00 - Time step 729 / time 5.98e-15s ( 5 % done), field decay: 1.00e+00 - Time step 976 / time 8.00e-15s ( 8 % done), field decay: 9.10e-01 - Time step 1464 / time 1.20e-14s ( 12 % done), field decay: 1.97e-01 - Time step 1952 / time 1.60e-14s ( 16 % done), field decay: 4.45e-02 - Time step 2440 / time 2.00e-14s ( 20 % done), field decay: 1.68e-02 - Time step 2928 / time 2.40e-14s ( 24 % done), field decay: 4.20e-03 - Time step 3416 / time 2.80e-14s ( 28 % done), field decay: 1.42e-03 - Time step 3904 / time 3.20e-14s ( 32 % done), field decay: 5.19e-04 - Time step 4392 / time 3.60e-14s ( 36 % done), field decay: 1.39e-04 - Time step 4880 / time 4.00e-14s ( 40 % done), field decay: 8.04e-05 - Time step 5368 / time 4.40e-14s ( 44 % done), field decay: 3.16e-05 - Time step 5856 / time 4.80e-14s ( 48 % done), field decay: 1.46e-05 - Time step 6344 / time 5.20e-14s ( 52 % done), field decay: 1.33e-05 - Time step 6832 / time 5.60e-14s ( 56 % done), field decay: 4.93e-06 Field decay smaller than shutoff factor, exiting solver. Solver time (s): 16.2193 Data write time (s): 0.0057
batch.real_cost()
21:07:41 -03 Total billed flex credit cost: 0.108.
0.10798620450705071
Step 9 - Result Analysis¶
After the simulations are complete, we can process the monitor data and compute the scattering efficiency. At the same time, you can compute the scattering coefficient analytically. To calculate the scattering cross section from the FDTD results, you can calculate the incident irradiance ($I_{i}$) as the flux_inj flux divided by the simulation domain area in the xy plane.
Use the code below to calculate the Mie efficiency from the analytical Mie theory.
Python: Use
sphere_n = np.sqrt(sphere_mat.eps_model(td.C_0 / lambdas))to calculate the sphere refractive indices.
# Compute the FDTD incident irradiance.
irradiance_i = batch_results["reference"]["flux_inj"].flux / source.size[0] / source.size[1]
# Compute the FDTD Mie scattering cross section.
scat_cross = batch_results["real"]["flux_out"].flux / irradiance_i
# Compute the sphere cross section area.
G = np.pi * (sphere_d / 2) ** 2
# Compute the FDTD Mie scattering efficiency.
Q_sca_fdtd = scat_cross / G
# Sphere refractive indices.
sphere_n = np.sqrt(sphere_mat.eps_model(td.C_0 / lambdas))
# Compute the Mie efficiency from the analytical Mie theory.
Q_sca_analytical = pms.MieQ_withWavelengthRange(
sphere_n, sphere_d * 1e3, wavelengthRange=lambdas * 1e3
)[2]
21:07:44 -03 loading simulation from data/fdve-4c6c7e28-6b2e-492f-88d3-9866b4aedad7.hdf5
21:07:45 -03 loading simulation from data/fdve-0083fda1-0d36-4690-b59d-a55674ff59f2.hdf5
GUI: After running the real and the reference simulations, you can export the flux monitor data to compare them with the analytical results.
Step 10 - Compare the FDTD and Analytical Results¶
Plot both FDTD and analytical results.
Python: Use
matplotlibto plot the results.
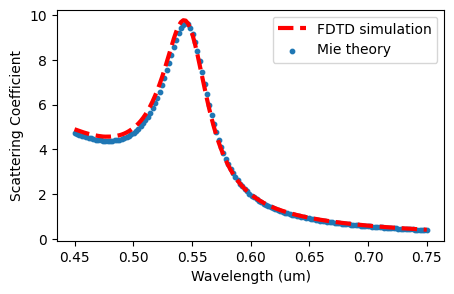
# Plot the simulation result and the analytical result
plt.figure(figsize=(5, 3))
plt.plot(lambdas, Q_sca_fdtd, linewidth=3, c="red", linestyle="--", label="FDTD simulation")
plt.scatter(lambdas, Q_sca_analytical, s=10, marker="o", label="Mie theory")
plt.xlabel("Wavelength (um)")
plt.ylabel("Scattering Coefficient")
plt.legend()
plt.show()
GUI: load the FDTD data into a Python notebook using
np.loadtxt(filename), and calculate the scattering efficiency.
Activity Description¶
Using the session notebook as a reference, calculate the scattering efficiency considering a single core-shell sphere nanoparticle. The core material is silicon ($n_{si} = 3.48$) with a diameter of 0.15 $\mu m$, and the shell is made of silica ($n_{sio2} = 1.45$) with a thickness of 0.075 $\mu m$. Keep the TFSF source, but set it to wavelengths from 0.45 $\mu m$ to 0.75 $\mu m$. Use 150 points to sample the optical response.
You can develop this example using the Tidy3D Python notebook or the Graphical User Interface (GUI) web-based environments.
You can use the code below as a reference to calculate the scattering efficiency. It calculates the refractive indices from the sphere core (sphere_mat_core) and shell (sphere_mat_shell) mediums, light wavelengths (lamdbas * 1e3), core (sphere_d_core) and shell (sphere_d_shell) diameters.
# Sphere core refractive indices.
sphere_n_core = np.sqrt(sphere_mat_core.eps_model(td.C_0 / lambdas))
# Sphere shell refractive indices.
sphere_n_shell = np.sqrt(sphere_mat_shell.eps_model(td.C_0 / lambdas))
# Compute the Mie efficiency from the analytical Mie theory.
Q_sca = []
for n_core, n_shell, wl in zip(sphere_n_core, sphere_n_shell, lambdas * 1e3):
Q_sca.append(pms.MieQCoreShell(
n_core, n_shell, wavelength=wl, dCore=sphere_d_core * 1e3, dShell=sphere_d_shell * 1e3)[1]
)
Q_sca_analytical = np.asarray(Q_sca)
References¶
[1] Craig F. Bohren and Donald R. Huffman. Absorption and Scattering of Light by Small Particles. John Wiley & Sons, Ltd; 1998. doi:10.1002/9783527618156